 |
 |
Математическая сДача |
26.02.2023 |
 |
Примеры заданий
 |
 |
«Выход есть!» -2023— конкурс по решению головоломок |
24.01.2023 |
 |
Примеры заданий - рус.
 |
 |
«Выход есть!» -2022— конкурс по решению головоломок |
30.01.2022 |
 |
Примеры заданий - рус.
Task examples - eng.
 |
 |
«Выход есть!» -2021— конкурс по решению головоломок |
22.01.2021 |
 |
Примеры заданий - рус.
Task examples - eng.
 |
 |
Примеры заданий |
25.08.2020 |
 |
Как научиться играть в SET
https://zen.yandex.ru/media/id/5d7a7d9e79c26e00ae521549/kak-nauchitsia-igrat-v-set-5ea99747ac8c3b48883f3dcb
Логические задачи (3-4)
https://zen.yandex.ru/media/id/5d7a7d9e79c26e00ae521549/logicheskie-zadachi-34-5d9cbe08d5bbc3391f43c503
Цифры и числа
https://zen.yandex.ru/media/id/5d7a7d9e79c26e00ae521549/cifry-i-chisla-3-5d7a7dd49c944600ae644048
 |
 |
«Выход есть!» — конкурс по решению головоломок |
06.02.2020 |
 |
 |
 |
«Выход есть!» — конкурс по решению головоломок |
06.01.2020 |
 |
Инструкции по решению задач
Instruction for task solutions
 |
 |
Инструкции к турниру «Выход есть!» |
12.01.2019 |
 |
Инструкции
 |
 |
«Выход есть!» — тексты и решения конкурса |
13.02.2018 |
 |
 |
 |
«Выход есть!» — примеры задач |
18.01.2018 |
 |
Примеры задач
 |
 |
Для школьников 1-4 классов
|
25.01.2017
|
 |
Тесты по математике для школьников 1-4 классов на следующие темы: логика, пространство, арифметика, текстовые задачи.
Регистрация - https://pelicanbook.ru/diagnostics/
Участие бесплатное.
 |
 |
«Выход есть!» — конкурс по решению головоломок |
21.10.2014 |
 |
Инструкции по решению задач
 |
 |
«Выход есть!» - конкурс по решению головоломок |
03.11.2013 |
 |
Инструкции ЗДЕСЬ
 |
 |
Разнобой - задачи с ранних матпраздников |
02.11.2013 |
 |
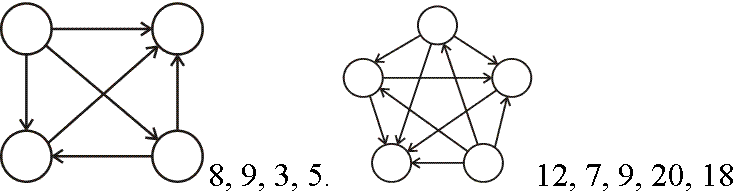
- Витя выложил из карточек пример на сложение, затем поменял местами две карточки: 314159 + 291828 = 585787. Как видите, равенство нарушилось. Какие карточки переставил Витя?
- Семья ночью подошла к мосту. Папа может перейти его за 1 минуту, мама - за 2, малыш - за 5, а бабушка - за 10 минут. У них есть один фонарик. Мост выдерживает только двоих. Как им перейти мост за 17 минут? (Если переходят двое, то они идут с меньшей из их скоростей)
- На глобусе проведены 17 параллелей и 24 меридиана. На сколько частей разделена поверхность глобуса? Меридиан – это дуга соединяющая Северный полюс с Южным. Параллель – это окружность, параллельная экватору.
- Расположите в вершинах правильного десятиугольника числа от 1 до 10 так, чтобы для любых двух соседних чисел их сумма была равна сумме двух чисел, им противоположных.
- Расставьте на шахматной доске 32 коня так, чтобы каждый из них бил ровно двух других.
- Нарисуйте на клетчатой бумаге треугольник с вершинами в углах клеток, две медианы которого перпендикулярны.
- На прямой отметили несколько точек. Потом между каждыми двумя соседними точками отметили по одной точке. Так сделали 3 раза, получилось 113 точек. Сколько точек было в начале?
- Если посмотреть на аквариум спереди, то траектория рыбки такая, как показана на левом рисунке. Если посмотреть справа – то как на правом. Нарисуй вид сверху.
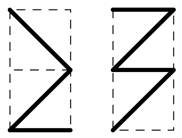
 |
 |
Осенний Олимп-2013
|
27.09.2013 |
 |
Математический конкурс
для 1-7 классов
1 класс 2 класс 3 класс 4 класс 5 класс 6 класс 7 класс
 |
 |
Математический конкурс «Весенний Олимп», 20-21 апреля 2013 года
|
16.05.2013 |
 |
Решение задач и головоломок про клады, путешествия на приз Золотой устрицы
Тексты заданий можно посмотреть здесь:
1 класс 2 класс 3 класс 4 класс 5 класс 6 класс 7 класс
 |
 |
Математическое путешествие по островам знаний «На пороге открытий»
|
03.03.2013 |
 |
16 февраля 2013 года прошел конкурс для детей 6-7 лет.
Тексты заданий и комментарии к ним можно посмотреть здесь
 |
 |
Осенний Олимп-2012
|
22.02.2013 |
 |
Математический конкурс
для 1-7 классов
(решение задач и головоломок про клады, путешествия
на приз Золотой устрицы)
Тексты заданий можно посмотреть здесь, а решения и ответы – в журнале «Квантик» №2 2013 год
читать дальше »
1 класс
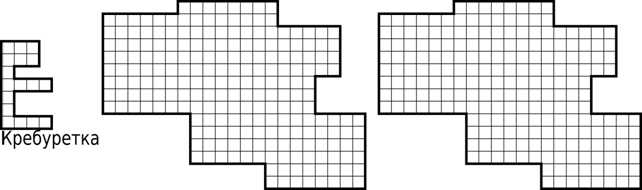
- Старый пират Джек поймал несколько странных животных и назвал их кребуретками. Размести в террариуме как можно больше кребуреток.

- Капитан Одноухий Мо купил несколько попугаев. По дороге на корабль половина попугаев разлетелась. Оставшихся он подарил приятелю. Вечером половина улетевших попугаев вернулась к Мо. В итоге у Мо оказалось 6 попугаев. Сколько попугаев купил Мо?
- В далёкую страну приехал путешественник. Он отличается от каждого жителя острова формой глаз, формой носа и формой лица. Обведи портрет путешественника.

- Капитан Джек заказал у портного брюки и китель. У портного есть красная, синяя и зелёная ткани. Каждая ткань бывает тёмная и светлая. Капитан не любит, когда верх и низ одновременно тёмные. Также он не любит, когда синее с зелёным вместе. Перечисли все подходящие Джеку костюмы, которые может сшить портной.
- Билл сложил квадратный платок пополам так, что получился прямоугольник. Его он разрезал по диагонали. Нарисуй на квадрате фигуры, на которые распался платок.

- Из клада, найденного на острове, капитан Флинт дал юным пиратам Биллу и Сэму по 2 золотые пластины. Но Флинт сказал, что они смогут забрать это золото себе насовсем, только если фигуры, которые каждый сложит из всех своих пластин, окажутся одинаковыми (одинаковые фигуры — равные по форме и размерам). Помоги юным пиратам сложить одинаковые фигуры (пластины можно поворачивать и переворачивать).

2 класс
- Старый пират Джек поймал несколько странных животных и назвал их кребуретками. Размести в террариуме как можно больше кребуреток.

- Капитан Одноухий Мо купил несколько попугаев. По дороге на корабль половина попугаев разлетелась. Половину оставшихся он подарил приятелю. Вечером половина улетевших попугаев вернулась к Мо. В итоге у Мо оказалось 4 попугаев. Сколько попугаев купил Мо?
- Из клада, найденного на острове, капитан Флинт дал юным пиратам Биллу и Сэму по 4 золотые пластины, но сказал, что они смогут забрать это золото себе насовсем, только если фигуры, которые каждый сложит из всех своих пластин, окажутся одинаковыми (одинаковые фигуры — равные по форме и размерам). Помоги юным пиратам сложить одинаковые фигуры (пластины можно поворачивать и переворачивать).

- Боб, Джек, Роб, Ян, Марк собираются в плавание. Но Боб отказывается плыть вместе с Марком, Роб поплывёт только тогда, когда поплывёт Марк, а Джек не поплывёт вместе с Яном, но только с Бобом. Набери как можно большую команду и выпиши её состав.
- Билл сложил квадратный платок пополам так, что получился прямоугольник. Его он разрезал по диагонали. Нарисуй на квадрате фигуры, на которые распался платок.

- Путешественник Магеллан ходит по сетчатому острову, записывая, сколько шагов он сделал. После каждого хода он поворачивал, при этом никакую точку не проходил дважды. От точки Н он дошёл до точки К. Вот список его ходов: 2, 2, 2, 2, 3, 3, 2. Восстанови его маршрут.

3 класс
- Старый пират Джек поймал несколько странных животных и назвал их кребуретками. Размести в террариуме как можно больше кребуреток.

- Капитан Одноухий Мо купил несколько попугаев. По дороге на корабль половина попугаев разлетелась. Половину оставшихся он подарил приятелю. Затем, пока он шёл на свой корабль, половину тех попугаев, которых он нёс, выпросил хозяин таверны. Вечером половина улетевших попугаев вернулась к Мо. В итоге у Мо оказалось 3 попугая. Сколько попугаев купил Мо?

- Из клада, найденного на острове, капитан Флинт дал юным пиратам Биллу и Сэму по 4 золотые пластины, но сказал, что они смогут забрать это золото себе насовсем, только если фигуры, которые каждый сложит из всех своих пластин, окажутся одинаковыми (одинаковые фигуры — равные по форме и размерам). Помоги юным пиратам сложить одинаковые фигуры (пластины можно поворачивать и переворачивать).
- Боб, Джек, Роб, Ян, Марк, Аврелий собираются в плавание. Но Боб отказывается плыть вместе с Марком, Джек вместе с Аврелием или Яном. Джек никуда не поплывёт без Роба, Роб никуда не поплывёт без Яна, Ян никуда не поплывёт без Марка. Набери как можно большую команду и выпиши её состав.
- Билл сложил квадратный платок пополам так, что получился прямоугольник. Его он разрезал по диагонали. На какие фигуры распался платок?
- Путешественник Магеллан ходит по сетчатому острову, записывая, сколько шагов он сделал. После каждого хода он поворачивал, при этом никакую точку не проходил дважды. От точки Н он дошёл до точки К. Вот список его ходов: 3, 3, 2, 2, 1, 3, 5, 1, 1, 2, 7. Восстанови его маршрут.

4 класс
- Старый пират Джек поймал несколько странных животных и назвал их кребуретками. Размести в террариуме как можно больше кребуреток.
- Капитан Одноногий Джек купил несколько бочек рома и принёс их на корабль. Каждый пират на корабле взял себе несколько бочек. Известно, что количество пиратов, взявших ровно две бочки, равно количеству бочек, взятых всеми остальными пиратами. То же можно сказать и про пиратов, взявших ровно одну бочку. Всего бочек было не больше 10. Сколько бочек купил капитан?

- Из клада, найденного на острове, капитан Флинт дал юным пиратам Биллу и Сэму по 4 золотые пластины, но сказал, что они смогут забрать это золото себе насовсем, только если фигуры, которые каждый сложит из всех своих пластин, окажутся одинаковыми (одинаковые фигуры — равные по форме и размерам). Помоги юным пиратам сложить одинаковые фигуры (пластины можно поворачивать и переворачивать).
- Боб, Джек, Роб, Ян, Марк, Аврелий собираются отправиться в кабак. Но Боб отказывается идти вместе с Марком, Джек вместе с Аврелием или Яном. Джек никуда не пойдёт без Роба, Роб никуда не пойдёт без Яна, Ян никуда не пойдёт без Марка. Какое наибольшее количество людей может отправиться в кабак?
- Билл сложил квадратный платок пополам так, что получился прямоугольник. Его он разрезал по диагонали. На какие фигуры распался платок?
- Путешественник Магеллан ходит по сетчатому острову, записывая, сколько шагов он сделал. После каждого хода он поворачивал, при этом никакую точку не проходил дважды. От точки Н он дошёл до точки К. Вот список его ходов: 3, 3, 2, 2, 1, 3, 5, 1, 1, 2, 7. Восстанови его маршрут.

5 класс
- Старый пират Джек скрестил улитку с компасом, получив странное существо — улимпаса. Домик улимпаса разделён на несколько комнат, при этом улимпас может переползать только в комнату, находящуюся справа или сверху от текущей. Сколькими способами улимпас может добраться до корма? (Разные способы — разные последовательности посещённых улимпасом комнат).
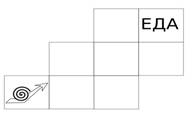
- Пираты собирались в плавание. Им нужно было закупить ром, мясо и порох. Капитан Джек велел повару Бобу купить 18 бочек рома, 26 бочек мяса и 52 бочки пороха (бочки с одинаковым содержимым весят одинаковое целое число килограмм). Когда Джек спросил у Боба, сколько весят бочки, Боб ответил: «Бочки с мясом и ромом вместе весят 842 килограмма, бочки с мясом и порохом — 686 килограмм, бочки с ромом и порохом — 742 килограмма, а всего вместе — ...» Повар не успел договорить, потому что капитан Джек взмахнул саблей и отрубил Бобу все пуговицы на рубашке. Как он догадался, что повар Боб неправильно выполнил его распоряжения?
- Пираты отправились в плавание. Через некоторое время весь провиант закончился, а ни одного корабля они так и не встретили. Тогда в отчаянии капитан обратился к своим попугаям за помощью.
— Надо плыть на север, — сказал первый попугай.
— Если мы поплывём на восток, то погибнем, — сказал второй попугай.
— Они оба врут, — сказал третий попугай.
— Все трое врут, — сказал четвёртый попугай.
— Ты врёшь, — сказал первый попугай четвёртому.
Капитан знает, что каждый из его попугаев либо всегда говорит правду, либо всегда врёт. Куда надо плыть?
- Пираты вдвоём взяли на абордаж корабль с золотом. Драться друг с другом у них не осталось сил, поэтому они разыграли добычу в карты. Они взяли две одинаковые колоды карт, тщательно перемешали, всю большую колоду поделили между собой как попало. Они договорились, что каждый из своей части выкинет пары одинаковых карт (по масти и достоинству), а тот, у кого после этого останется меньше карт, отдаст свою долю победителю. Верно ли, что в такой игре игрок, взявший больше карт, всегда побеждает?
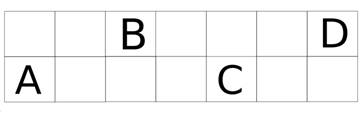
- После успешного абордажа пираты стали делить золото. К сожалению, справедливого дележа не получилось, и обиженные пираты высадили капитана на необитаемый остров. Чтобы выжить, капитану пришлось заняться выращиванием репы. Грядка представляет собой прямоугольник 2 x 7 клеток. Когда Джек сажает семечко в клетку, в этой клетке, а также во всех, соседних с ней по стороне, вырастает по репе. В клетках A, C и D выросло 11, 12 и 13 реп соответственно. Сколько реп выросло в клетке B, если всего капитан посадил 65 семечек?
6 класс
- У старого пирата Джека живет странное существо — улимпас. Домик улимпаса разделён на несколько комнат, при этом улимпас может переползать только в комнату, находящуюся справа или сверху от текущей. Сколькими способами улимпас может добраться до корма? (Разные способы — разные последовательности посещённых улимпасом комнат).
- Пираты собирались в плавание. Им нужно было закупить ром, мясо и порох. Капитан Джек велел повару Бобу купить хотя бы 2 бочки пороха и хотя бы 2 бочки рома. Рассказывая капитану о покупке, Боб похвастался: «Представляешь, я настолько удачно купил провиант, что количество бочек пороха и мяса вместе оказалось простым числом. Общее количество бочек пороха и рома тоже простое. И даже бочек рома и мяса в сумме — простое число!» Повар не успел договорить, потому что капитан Джек взмахнул саблей и отрубил Бобу все пуговицы на рубашке. Как он догадался, что повар Боб неправильно выполнил его распоряжения?
- Пираты отправились в плавание. Через некоторое время весь провиант закончился, а ни одного корабля они так и не встретили. Тогда в отчаянии капитан обратился к своим попугаям за помощью.
— Надо плыть на север, — сказал первый попугай.
— Если мы поплывём на восток, то погибнем, — сказал второй попугай.
— Они оба врут, — сказал третий попугай.
— Все трое врут, — сказал четвёртый попугай.
— Ты врёшь, — сказал первый попугай четвёртому.
Капитан знает, что каждый из его попугаев либо всегда говорит правду, либо всегда врёт. Куда надо плыть?
- Пираты вдвоём взяли на абордаж корабль с золотом. Драться друг с другом у них не осталось сил, поэтому они разыграли добычу в карты. Они взяли две одинаковые колоды карт, тщательно перемешали, всю большую колоду поделили между собой как попало. Далее каждый из них ищет среди своих карт пары одинаковых (по масти и достоинству), одну карту из каждой пары отдаёт сопернику, другую скармливает своему попугаю. Тот, у кого после этого останется меньше карт, отдаёт свою долю победителю. Верно ли, что в такой игре игрок, взявший изначально карт меньше, чем соперник, всегда побеждает?
- После успешного абордажа пираты стали делить золото. К сожалению, справедливого дележа не получилось, и обиженные пираты высадили капитана на необитаемый остров. Чтобы выжить, капитану пришлось заняться скотоводством. Чтобы разводить гусей, нужен забор, огораживающий площадь не менее 25 м2. Для разведения свиней требуется хотя бы 35 м2. Для разведения коров — хотя бы 40 м2. У капитана есть доски с гвоздями, из которых можно сделать забор длиной не более 56 м. Сможет ли он разводить все 3 вида животных? (Разных животных нельзя держать на одной территории).
7 класс
- У старого пирата Джека живет странное существо — улимпас. Домик улимпаса разделён на несколько комнат, при этом улимпас может переползать только в комнату, находящуюся справа или сверху от текущей. Сколькими способами улимпас может добраться до корма? (Разные способы — разные последовательности посещённых улимпасом комнат).
- Пираты собирались в плавание. Им нужно было закупить ром, мясо и порох. Капитан Джек велел повару Бобу купить хотя бы 2 бочки пороха и хотя бы 2 бочки рома. Рассказывая капитану о покупке, Боб похвастался: «Представляешь, я настолько удачно купил провиант, что количество бочек пороха и мяса вместе оказалось простым числом. Общее количество бочек пороха и рома тоже простое. И даже бочек рома и мяса в сумме — простое число!» Повар не успел договорить, потому что капитан Джек взмахнул саблей и отрубил Бобу все пуговицы на рубашке. Как он догадался, что повар Боб неправильно выполнил его распоряжения?
- Пираты отправились в плавание. Через некоторое время весь провиант закончился, а ни одного корабля они так и не встретили. Тогда в отчаянии капитан обратился к своим попугаям за помощью.
— Надо плыть на север, — сказал первый попугай.
— Если мы поплывём на восток, то погибнем, — сказал второй попугай.
— Они оба врут, — сказал третий попугай.
— Все трое врут, — сказал четвёртый попугай.
— Ты врёшь, — сказал первый попугай четвёртому.
Капитан знает, что каждый из его попугаев либо всегда говорит правду, либо всегда врёт. Куда надо плыть?
- Пираты взяли на абордаж корабль с золотом. Перед атакой капитан несколько раз попытался поставить пиратов в k рядов так, чтобы в рядах было поровну пиратов. Выяснилось, что при k от 2 до 10 включительно остаётся хотя бы k/2 лишних пиратов. Какое наименьшее количество пиратов могло пойти на абордаж?
- После успешного абордажа пираты стали делить золото. К сожалению, справедливого дележа не получилось, и обиженные пираты высадили капитана на необитаемый остров. Чтобы выжить, капитану пришлось заняться скотоводством. Чтобы разводить гусей, нужен забор, огораживающий площадь не менее 25 м2. Для разведения свиней требуется хотя бы 35 м2. Для разведения коров — хотя бы 40 м2. У капитана есть доски с гвоздями, из которых можно сделать забор длиной не более 56 м. Сможет ли он разводить все 3 вида животных? (Разных животных нельзя держать на одной территории).
 |
 |
Инструкции к конкурсу «Выход есть!»
|
18.11.2012 |
 |
читать дальше »
Условия задач турнира решателей головоломок «Выход есть!» 16 декабря 2012 года.
В задачах вам предстоит найти маршрут по лабиринту. Будьте внимательны – правила для каждого лабиринта свои.
Классический
Найдите кратчайший путь от одного входа до другого. Нарисуйте ваш маршрут. |
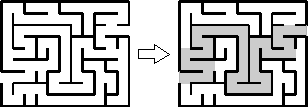
|
|
|
Замкнутый маршрут
Проведите линию, состоящую из горизонтальных и вертикальных отрезков, которая проходит через все клетки квадрата по одному разу. Стены, отмеченные жирной линией пересекать нельзя. |
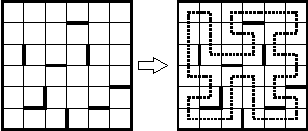
|
|
|
Подземный ход
Под землей проложен ход – линия шириной в одну клетку, которая не касается себя даже углом. Вход и выход показаны. Числа вокруг сетки показывают количество клеток, занятых подземным ходом в соответствующем ряду. |
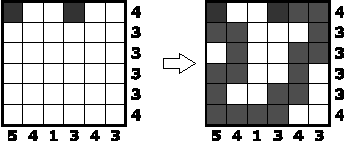
|
|
|
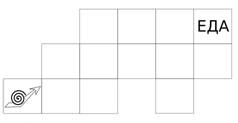
Кузнечик
Начав с левой верхней клетки, кузнечик должен посетить все клетки по одному разу и закончить в правой нижней. Из клетки кузнечик может прыгнуть на любое расстояние в направлении стрелки. Пронумеруйте клетки в порядке посещения. |
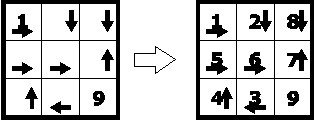
|
|
|
Шахматный
Найдите путь из левой верхней клетки в правую нижнюю так, чтобы в пути следования светлые и темные клетки чередовались. |
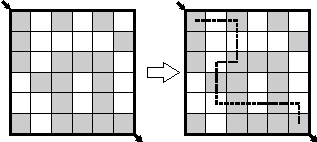
|
|
|
Магический
Впишите в некоторые клетки буквы так, чтобы при следовании по лабиринту от входа до тупика несколько раз читалось указанное слово. Буквы должны встречаться ровно один раз в каждой строке и в каждом столбце. |
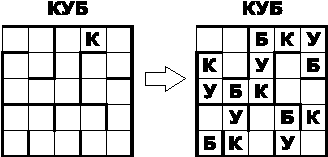
|
|
|
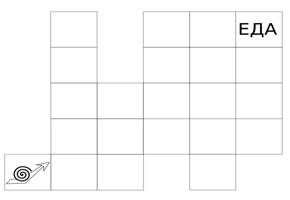
Автомобильный
Начав с одной из стоянок (отмечены буквой P) проложите маршрут, закончив его на другой стоянке. Вы должны посетить все магазины (отмечены буквой S) и все стоянки. Два раза по одному участку или по одному перекрестку проезжать нельзя. Стрелками отмечены улицы с односторонним движением. |
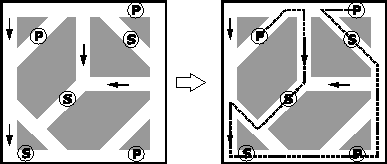
|
|
|
Пятнадцать
Найдите путь из левой верхней клетки в правую нижнюю посетив по пути все серые клетки. Сумма цифр, посещенных между двумя серыми клетками должна быть равна 15. |
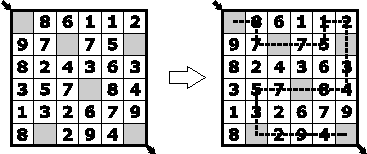
|
 |
 |
Математический конкурс "По морям, по волнам" на приз Золотой Устрицы |
06.03.2011 |
 |
5 класс. 27 февраля 2011 года. МГДДюТ
читать дальше »
- На острове Выйгач живут три племени: рыбаки, которые говорят только правду; хитряки, которые всегда лгут, простаки, которые говорят правду, если до его фразы была сказана правда, ложь, если до его фразы была сказана ложь, а если начинают разговор первыми, могут сказать что угодно - и правду, и ложь. Встретились три представителя от каждого племени, и между ними состоялся следующий разговор: 1-ый : "Оба вы пираты". 2-ой : "Да, 3-ий - пират". 3-ий : "Я - не пират". 1-ый : "Мы с 3-им из одной деревни". 3-ий : "Я - не простак". 2-ой : "Я – не хитрец". 1-ый : "И я – не хитрец". Определите, кто есть кто, если у каждого племени - своя деревня. (Устно)
- Пират Назойливый Ефим провинился. Его решили выбросить за борт. Когда Ефима сбрасывают в воду, он за 9 секунд всплывает вверх и за 6 секунд догоняет корабль, залезает обратно на палубу. Его обратно сбрасывают, он опять возвращается… И так далее. Команде это надоело, и корабль поплыл в 2 раза быстрее. Сколько секунд теперь потребуется Ефиму, чтобы догнать корабль после всплытия на поверхность? (Устно)
- Четыре пирата нашли клад, состоящий из монет достоинством 1, 2, 5 и 10 дублонов. Они договорились, что каждый заберёт себе все монеты какого-то одного достоинства. Монет достоинством 1 дублон в пять раз больше, чем монет достоинством 5 дублонов и 10 дублонов вместе, а монет достоинством 2 дублона столько же, сколько всех остальных. Первым берёт главарь Монеты какого достоинства ему выгоднее забирать? (Устно)
- Капитан Ефим отправился в плавание, купив календарь. Оказалось, что в каждом году пропущен февраль, то есть, сразу после 31 января идёт 1 марта. Капитан обратил внимание на 2 подряд идущих года. В первом понедельников больше, чем сред. Какой день недели чаще всего встречается во втором году? (Письменно)
- У пирата Ефима есть 3 морских волка и 3 морские свинки. Он пытается переправится через реку в лодке, в которую вместе с ним помещаются ещё два животных. Если число волков на каком-либо берегу превышает число свинок, то волки весело поедают бедных свинок.При каждой переправе в лодке есть хотя бы одно животное. Каким должен быть план перевозок, чтобы после переправы все животные остались в живых? (Письменно)
- Капитан Рукастый Ефим сделал замечательный квадратный плот со сторонами в 60 локтей и отправился в кругосветное плавание. Только он отплыл от берега, плот развалился на 3 части одинаковой площади и прямоугольной формы. Известно, что любые 2 части изначально соприкасались. Найдите общую длину разломов. (Письменно)
6 класс. 27 февраля 2011 года. МГДДюТ
читать дальше »
- На острове Выйгач живут три племени: рыбаки, которые говорят только правду; хитряки, которые всегда лгут, простаки, которые говорят правду, если до его фразы была сказана правда, ложь, если до его фразы была сказана ложь, а, если начинают разговор первыми, могут сказать что угодно - и правду, и ложь. Встретились три представителя от каждого племени, и между ними состоялся следующий разговор: 1-ый: "Оба вы пираты". 2-ой : "Да, 3-ий - пират". 3-ий : "Я - не пират". 1-ый : "Мы с 3-им из одной деревни". 3-ий : "Я - не простак". 2-ой : "Я – не хитрец". 1-ый : "И я – не хитрец". Определите, кто есть кто, если каждое племя живёт в своей деревне. (Устно)
- Пираты Ефим и Фома вышли одновременно из таверны "Одинокая каракатица". Шаг Ефима равен 60 см, а шаг Фомы равен 69 см. В первый раз их шаги совпали через 17 секунд после начала движения. А когда после 5 минут движенияих шаги у пиратов совпали первый раз, то они стояли на пороге таверны "Кривой попугай". Каково расстояние между двумя тавернами? (Устно)
- Четыре пирата нашли клад, состоящий из монет достоинством 1, 2, 5 и 10 дублонов. Они договорились, что каждый заберёт себе все монеты какого-то одного достоинства. Монет достоинством 1 дублон в пять раз больше, чем монет достоинством 5 дублонов и 10 дублонов вместе, а монет достоинством 2 дублона столько же, сколько всех остальных. Первым берёт главарь Монеты какого достоинства ему выгоднее забирать? (Устно)
- Капитан Ефим отправился в плавание, купив календарь. Оказалось, что в каждом году пропущен февраль, то есть сразу после 31 января идёт 1 марта. Капитан обратил внимание на 2 подряд идущих года. В первом понедельников больше, чем сред. Какой день недели чаще всего встречается во втором году? (Письменно)
- Нарисовать на клетчатой бумаге треугольник и шестиугольник с вершинами в узлах сетки такие, что периметр и площадь треугольника равны соответственно периметру и площади шестиугольника. (Письменно)
- У пирата Ефима есть 3 морских волка и 3 морские свинки. Он пытается переправится через реку в лодке, в которую вместе с ним помещаются ещё два животных. Если число волков на каком-либо берегу превышает число свинок, то волки весело поедают бедных свинок.При каждой переправе в лодке есть хотя бы одно животное. Каким должен быть план перевозок, чтобы после переправы все животные остались в живых? (Письменно)
 |
 |
Ответы и решения задач математического конкурса "По морям, по волнам"! |
03.03.2011 |
 |
читать дальше »
Жюри оставляет право за школьником приводить другое решение задачи.
№1. Пусть первый --- рыбак. Тогда второй и третий --- пираты. Значит, третий --- хитрец, но хитрец не может сказать "Я не простак". Противоречие.
Пусть первый --- хитрец. Тогда второй не может быть рыбаком: в этом случае третий был бы простаком и не мог бы сказать, что он не пират, т.к. эта фраза сказана за правдивой фразой. Значит, второй --- простак, а третий --- рыбак (нетрудно убедиться, что при этом разговор непротиворечив).
Пусть первый --- простак. Тогда второй не хитрец (т.к. его последняя фраза правдива). Значит, второй --- рыбак, а третий --- хитрец. Но хитрец не может сказать, что он не простак. Противоречие.
Ответ: Первый --- хитрец, второй --- простак, третий --- рыбак.
№ 2, 5 класс. Изначально корабль за 15 секунд преодолевает то же расстояние, что и Ефим за 6. Теперь Ефиму на расстояние, преодолеваемое кораблём за 15 секунд, требуется уже 12 секунд. Пусть за 15 секунд корабль проходит 60 условных единиц длины. Тогда его
скорость --- 4 уе/сек, а скорость Ефима --- 5 уе/сек. Скорость сближения равна 1 уе/сек, а на момент всплытия Ефима и корабль разделяют 36 уе. Значит, через 36 секунд Ефим догонит корабль.
Ответ: 36 секунд.
№2, 6класс. За 17 секунд пираты проходят одинаковое расстояние --- наименьшее общее кратное 60 см и 69 см. Оно равно 1380 см. Каждые 17 секунд пираты ставят ноги на землю одновременно. Наименьшее число, кратное 17 и большее 300, равно 306=17*18. За 306 секунд, соответственно, пираты пройдут 18*1380 = 24840 см.
Ответ: 24840 см.
№ 3. Надо брать монеты достоинством 2 дублона. Их стоимость в дублонах больше, чем удвоенное количество монет достоинством 1 дублон, равное удесятерённому количеству десятидублонных монет (их суммарной стоимости) плюс удесятерённому количеству пятидублонных монет (их удвоенной суммарной стоимости).
Ответ: Надо брать монеты достоинством 2 дублона.
№4. В году без февраля 365-28 = 337 дней. 337 = 7*48 + 1, поэтому в году 48 полных недель (начинающихся с того дня недели, которым было 1 января) и ещё один день (соответствующий ему день недели и встречается чаще других) --- 31 декабря. В первом году этот день, очевидно, понедельник. Значит, 1 января в следующем году --- вторник. 31 декабря, соответственно, тоже вторник.
Ответ: Вторник.
Критерии:
3 балла --- полное решение
2 балла --- объяснено, почему день недели 1 января/31 декабря встречается чаще других, но ответ по какой-то причине неверный/отсутствует
1 балл --- голый ответ
№ 5. Один из способов (знаки & разделяют берега и содержимое лодки):
BBBCCC & &
BBCC & BC &
BBBCCC & &
BBCC & BC &
BBCC & C & B
BCC & BC & B
BCC & B & BC
BC & BC & BC
BC & B & BCC
C & BB & BCC
C & B & BBCC
& BC & BBCC
& & BBBCCC
Критерии:
3 балла --- верное решение
№6, 5 класс. Части имеют размеры 20x60, 40x30, 40x30. То, что две части имеют одно из измерений, равное 30, очевидно. Если другое измерение этих частей равно y локтей, то третья часть имеет размер (60-y)*60. Из условия равенства площадей получаем уравнение
3600 - 60y = 30y, откуда y = 40. Общая длина разлома, соответственно, равна 60 + 40 = 100.
Ответ: 100 локтей.
Критерии:
+1 балл: верный ответ
+1 балл: показано верное расположение частей
+1 балл: правильно определены размеры частей
№6, 6класс. Один из возможных примеров приведён на рисунке. Если разрезать левую фигуру по розовой линии и склеить из полученных частей
фигуру, изображённую на правом рисунке, периметр не изменится, т.к. длина образовавшихся при разрезании сторон равна длине сторон, исчезнувших после склейки.
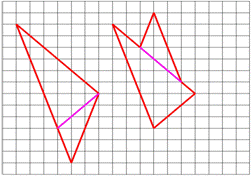
Критерии:
3 балла --- верный пример с доказательством равенства периметров и площадей
2 балла --- верный пример, но не доказано одно из равенств (периметров или площадей)
1 балл --- только верный пример
 |
 |
"Осенний Олимп"
Математический конкурс на приз Большого кованого гвоздя |
15.02.2011 |
 |
1 класс
читать дальше »
- У Змея Горыныча на огороде растёт морковка. Между некоторыми грядками забор. Помогите Змею Горынычу собрать морковку, побывав на каждой грядке не более одного раза.
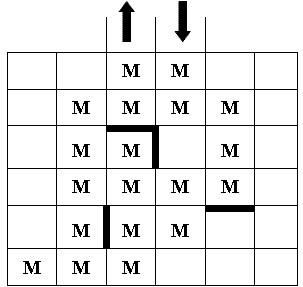
- Стрелка идёт от большего числа к меньшему:
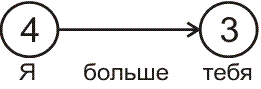
Впишите числа в кружочки так, чтобы получилось правильно.
- Кубик весит как два мячика и один ржавый замок в 3 кг. А ещё кубик весит как 3 мячика и не ржавый замок в 2 кг. Сколько весит кубик ?

- В волшебном зеркале отражаются невидимые предметы. Дорисуй их. Подумай и дорисуй, что должно быть в последнем зеркале.
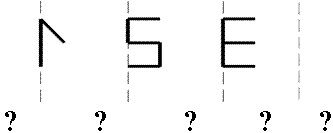
- Иван старше Марьи на 2 года. Вместе им через 3 года будет 12 лет. Сколько лет Марье?
2 класс
читать дальше »
- У Змея Горыныча на огороде растёт морковка. Между некоторыми грядками забор. Помогите Змею Горынычу собрать морковку, побывав на каждой грядке не более одного раза.
- Стрелка идёт от большего числа к меньшему:
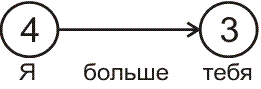
Впишите числа в кружочки так, чтобы получилось правильно.

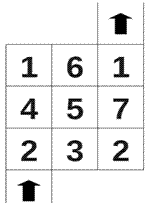
- В дремучем лесу витязь нашёл заброшенный дворец. На пороге лежало 4 монет, а в каждой комнате столько, сколько написано на рисунке. Для того, чтобы открыть любую дверь, надо в замок опустить две монеты. Как только витязь проходит через дверь, она закрывается навсегда. Нарисуйте путь витязя, если он вышел, имея 6 монет.
- В волшебном зеркале отражаются невидимые предметы. Дорисуй их. Подумай и дорисуй, что должно быть в последнем зеркале.
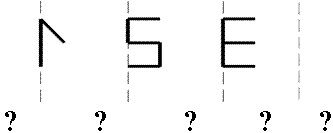
- В жаркий день 6 купцов выпили бочонок кваса за 3 часа. Нужно узнать, сколько купцов за 6 часов выпьют такой же бочонок кваса.
- Брат старше сестры на 2 года. Год назад им вместе было столько лет, сколько брату будет через два года. Сколько лет будет брату, когда его сестра будет такого возраста, как он сейчас?
3 класс
читать дальше »
- У Змея Горыныча на огороде растёт морковка. Между некоторыми грядками забор. Помогите Змею Горынычу собрать морковку, побывав на каждой грядке не более одного раза.
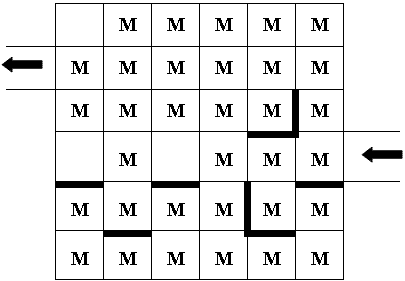
- В волшебном зеркале частично отражаются частично видимые буквы. Дорисуй их, выпиши в ответ имя, которое получилось.
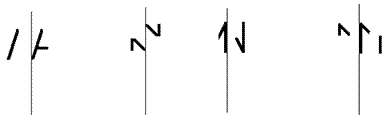
- Стрелка идёт от большего числа к меньшему:
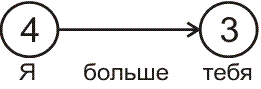
Впишите числа в кружочки так, чтобы получилось правильно.
- В жаркий день 6 купцов выпили бочонок кваса за 3 часа. Нужно узнать, сколько купцов за 6 часов выпьют такой же бочонок кваса.
- Баба Яга решила поменять имена своим слугам. Получилось так:

Заполни пропуски в таблице.
- Брат старше сестры на 2 года. Год назад им вместе было столько лет, сколько брату будет через два года. Сколько лет будет брату, когда его сестра будет такого возраста, как он сейчас?
4 класс
читать дальше »
- У Змея Горыныча на огороде растёт морковка. Между некоторыми грядками забор. Помогите Змею Горынычу собрать морковку, побывав на каждой грядке не более одного раза.
- В волшебном зеркале частично отражаются частично видимые буквы. Дорисуй их, выпиши в ответ имя, которое получилось.

- Стрелка идёт от большего числа к меньшему:
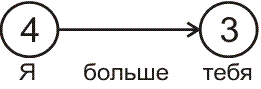
Впишите числа в кружочки так, чтобы получилось правильно.

- Разносчик купил несколько апельсинов. Если он будет продавать их по 9 копеек за штуку, то получит (20 копеек) прибыли в копейках в два раза больше чем, убыток, который понесёт если же будет продавать по 6 копеек(, то понесёт 10 копеек убытку). Какое наименьшее количество апельсинов мог купить разносчик?
- Разносчик купил несколько апельсинов. Если он будет продавать их по 9 копеек за штуку, то получит (20 копеек) прибыли в копейках в два раза больше чем, убыток, который понесёт если же будет продавать по 6 копеек(то понесёт 10 копеек убытку). Какое наименьшее количество апельсинов мог купить разносчик?
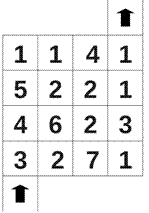
- Плата работнику за 30 дней – 81 динар и платье. Он работал 3 дня и заработал платье. Сколько стоит платье ?
 |
 |
Обещанная задача |
17.10.2010 |
 |
читать дальше »
Нарисуйте шестизвенную замкнутую ломаную, каждое звено которой ровно один раз пересекается с каким-то другим звеном этой же ломаной.
Ответ:
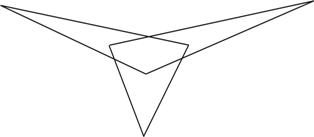
 |
 |
Олимпиада по математике 1-7 классов "Весенний Олимп"
Московского городского Дворца детского и юношеского творчества (21.03.2010) |
24.08.2010 |
 |
1 класс (1 вариант)
читать дальше »
- Раздели эту фигуру на три одинаковые по форме и размеру части.

- Витя и Таня ходят в штанах, а Лиза – в юбке. У Лизы и Тани одежда в клетку, а у Вити – в полоску. У кого из ребят не юбка и не в полоску?
- Два яблока весят столько же, сколько 3 груши. Что тяжелее: 8 груш или 6 яблок?

- Маша сидит на четвёртой парте спереди, и её парта предпоследняя. Сколько всего парт в ряду?
-
- В инкубаторе было 9 яиц. Из некоторых вылупились питончики, а из остальных – крокодильчики. В сумме у детёнышей оказалось 12 ног. Сколько вылупилось питончиков?
- Миша родился на 3 года раньше Гриши. А Гриша – на 1 год позже Даши. Кто старше – Даша или Миша и на сколько?
- У Кати и Вари вместе 7 кукол. Сколько кукол у каждой девочки, если у Вари на 3 куклы больше, чем у Кати?
- В примере на сложение двух чисел первое слагаемое меньше суммы на 40, а сумма больше второго слагаемого на 20. Восстановите пример.
2 класс (2 вариант)
читать дальше »
- Миша сидит на четвёртой парте спереди, и его парта предпоследняя. Сколько детей сидит за этими партами, если за каждой партой сидит 2 человека?
- Чтобы открыть дверь в пещеру с сокровищами, Али Бабе нужно расставить 4 магических фигуры в волшебной таблице так, чтобы в каждой строке и в каждом столбце встречались все 4 фигуры. Какую фигуру надо поставить в серую клеточку?
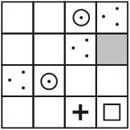
- Сергей Александрович назвал дочку в честь своего отца. Напишите имя и отчество его дочери.
- Один мишка весит столько же, сколько 3 собаки. Кто тяжелее: 6 собак или 3 мишки?

- Миша родился на 3 года раньше Гриши. А Гриша – на 1 год позже Даши. Кто старше – Даша или Миша и на сколько?
- Первого апреля на родительское собрание пришли учительница математики, учительница физики и учительница химии. Анна Борисовна сказала: "Я веду химию". Татьяна Николаевна: "Виктория Петровна ведёт химию". Виктория Петровна: "Я веду физику". Одна из них пошутила. Кто ведёт математику?
- Каждые 3 метра дедушка вкапывает столбик и строит между ними забор. Сколько столбиков он вкопал, чтобы построить забор длиной 12 м?
- В одной квартире живут люди и кошки. Всего у них 14 глаз и 22 ноги. Кого больше: людей или кошек и на сколько?
- В примере на сложение двух чисел первое слагаемое меньше суммы на 43, а сумма больше второго слагаемого на 34. Восстановите пример.
- Прямоугольник разбит на квадраты. Найди периметр прямоугольника, если периметр закрашенного квадрата равен 8 см.

3 класс (1 вариант)
читать дальше »
- Собака в 2 раза тяжелее кошки. Кто легче: 12 кошек или 3 собаки и во сколько раз?
- Раздели эту фигуру на три одинаковые по форме и размеру части.
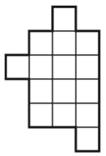
- Коля пригласил Петю в гости, сказав, что живёт в квартире № 117, а этаж сказать забыл. Подойдя к дому, Петя обнаружил, что дом девятиэтажный и на каждом этаже по 4 квартиры. На какой этаж ему следует подняться?
- В доме живёт трое домовых: Борис Николаевич, Василий Петрович и Аркадий Борисович. Один из них ежедневно прячет мобильный телефон хозяина. Борис Николаевич сказал: "Телефон прячет Василий Петрович". Василий Петрович: "Телефон прячет Аркадий Борисович". Аркадий Борисович: "Я прячу телефон". Только один домовой сказал правду. Кто прячет телефон?
- Коля рассказывал: “Нас в семье три брата. Я родился на 3 года раньше Пети, а Петя – на 5 лет позже Вани. Когда младшему из нас исполнилось 7 лет, родилась у нас сестра Люся”. На сколько лет Коля старше Люси?
- В инкубаторе лежало 21 яйцо. Из некоторых вылупились утята, а из остальных – утконосы, причём ног и у тех, и у других оказалось поровну. Сколько вылупилось утят?
- Лифт поднимается с первого этажа на пятый за 25 секунд. За какое время лифт поднимается с первого этажа на девятый?
- Кролик хочет разложить 25 морковок в 10 корзинок так, чтобы в каждой корзинке была либо 1, либо 3, либо 5 морковок. Как ему это сделать?
- Прямоугольник разбит на квадраты. Найди периметр и площадь прямоугольника, если периметр закрашенного квадрата равен 12 см.
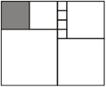
3 класс (2 вариант)
читать дальше »
- Яблоко в 3 раза тяжелее сливы. Что легче: 12 слив или 2 яблока и во сколько раз?
- Раздели эту фигуру на три одинаковые по форме и размеру части.
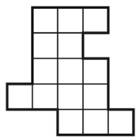
- Катя пригласила Машу в гости, сказав, что живёт в квартире № 125, а этаж сказать забыла. Подойдя к дому, Маша обнаружила, что дом 12-этажный и на каждом этаже по 4 квартиры. На какой этаж ей следует подняться?
- В пруду живут три русалки: Екатерина Петровна, Татьяна Ивановна и Анна Борисовна. Этой ночью одна из них пела задушевную песню с вершины дуба. Екатерина Петровна сказала: "Это была Татьяна Ивановна". Татьяна Ивановна: "Это пела Анна Борисовна". Анна Борисовна: "Это я пела!" Только одна русалка сказала правду. Кто пел песню этой ночью?
- Надя рассказывала: “У меня две сестры. Я родилась на 3 года раньше Любы, а Люба – на 4 года позже Веры. Когда младшей из нас было 6 лет, родился Сева". На сколько лет Надя старше Севы?
- Катя заботится о котятах и цыплятах. Лап у котят столько же, сколько у цыплят, а глаз в сумме 36. Сколько котят у Кати?
- Лифт поднимается с первого этажа на четвёртый за 8 секунд. За какое время лифт поднимается с первого этажа на шестнадцатый?
- Лена хочет раздарить 25 тюльпанов шести своим подружкам так, чтобы каждой досталось либо 3, либо 5, либо 7 тюльпанов. Как ей это сделать?
- Прямоугольник разбит на квадраты. Найди периметр и площадь прямоугольника, если периметр закрашенного квадрата равен 16 см.
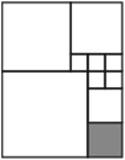
4 класс (1 вариант)
читать дальше »
- Раздели эту фигуру на три одинаковые по форме и размеру части.

- В доме живёт трое домовых: Борис Николаевич, Василий Петрович и Аркадий Борисович. Один из них ежедневно прячет мобильный телефон хозяина. Борис Николаевич сказал: "Телефон прячет Василий Петрович". Василий Петрович: "Телефон прячет Аркадий Борисович". Аркадий Борисович: "Я прячу телефон". Только один домовой сказал правду. Кто прячет телефон?
- Бабушка решила разместить 8 козлят и 9 гусят в пяти хлевах так, чтобы в каждом хлеву были и козлята, и гусята, а число ног равнялось 10. Как ей это сделать?
- Жеребёнок весит на 4 кг больше, чем ягнёнок. 2 жеребёнка весят столько же, сколько 3 ягнёнка. Сколько весит жеребёнок?
- Костя рассказывал: “У меня два брата. Я родился на 2 года раньше Феди, а Федя – на 3 года позже Дани. Когда младшему из нас было 5 лет, родилась Маша". На сколько лет Костя старше Маши?
- В некотором стаде зуброкроков и крокозубров 69 ног и 19 голов. У зуброкрока 15 ног и 1 голова, а у крокозубра 4 головы. Сколько в этом стаде существ?
- Маша и Коля живут в одном доме, Маша – на 4-м этаже, а Коля – на 16-м. Поднимаясь к себе домой по лестнице, Маша насчитала 24 ступеньки. Сколько шагов понадобится Коле, чтобы спуститься из дома на улицу, если он прыгает через 2 ступеньки?
- У бабушки в саду больше 70, но меньше 80 кустов. Третья часть из них – малина, четверть – крыжовник, а остальные – смородина. Сколько кустов смородины в саду у бабушки?
- Прямоугольник разбит на квадраты. Найди периметр и площадь прямоугольника, если площадь закрашенного квадрата равна 100 кв.см.
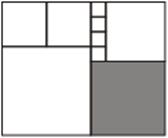
4 класс (2 вариант)
читать дальше »
- Раздели эту фигуру на три одинаковые по форме и размеру части.

- В пруду живут три русалки: Екатерина Петровна, Татьяна Ивановна и Анна Борисовна. Этой ночью одна из них пела задушевную песню с вершины дуба. Екатерина Петровна сказала: "Это была Татьяна Ивановна". Татьяна Ивановна: "Это пела Анна Борисовна". Анна Борисовна: "Это я пела!" Только одна русалка сказала правду. Кто пел песню этой ночью?
- Бабушка решила разместить 8 козлят и 9 гусят в пяти хлевах так, чтобы в каждом хлеву были и козлята, и гусята, а число ног равнялось 10. Как ей это сделать?
- Мешок яблок на 2 килограмма тяжелее мешка груш. 3 мешка яблок весят столько же, сколько 4 мешка груш. Сколько весит мешок яблок?
- Надя рассказывала: “У меня две сестры. Я родилась на 3 года раньше Любы, а Люба – на 4 года позже Веры. Когда младшей из нас было 6 лет, родился Дима." На сколько лет Надя старше Димы?
- В некотором стаде зуброкроков и крокозубров 69 ног и 19 голов. У зуброкрока 15 ног и 1 голова, а у крокозубра 4 головы. Сколько в этом стаде крокозубров?
- Маша и Коля живут в одном доме, Маша – на 3-м этаже, а Коля – на 9-м. Поднимаясь к себе домой по лестнице, Маша насчитала 18 ступенек. Сколько шагов понадобится Коле, чтобы спуститься из дома на улицу, если он прыгает через 2 ступеньки?
- У дедушки в саду больше 90, но меньше 100 деревьев. Третья часть из них – вишни, четверть – сливы. А остальные – яблони. Сколько яблонь в саду у дедушки?
- Прямоугольник разбит на квадраты. Найди периметр и площадь прямоугольника, если площадь закрашенного квадрата равна 64 кв.см.
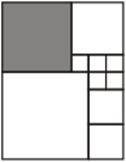
5 класс
читать дальше »
- Назовем фигуру, нарисованную на клетчатой бумаге по линиям сетки, "хорошей", если ее можно разрезать на доминошку в 2 клетки и уголок из 3 клеток. Ефим коллекционирует "нехорошие" фигуры. В "нехорошей" фигуре каждая клетка имеет хотя бы одну общую сторону с другой клеткой. Нарисуйте как можно больше "нехороших" фигур из 5 клеток для коллекции Ефима.
- Ефим пригласил на чаепитие 6 коллекционеров и посадил их за круглый стол. Все коллекционеры либо лжецы, которые всегда врут, либо рыцари,которые всегда говорят правду. Каждый сидящий на четном месте гордо заявил: "Я - рыцарь!". Каждый сидящий на нечетном месте сказал: "Ровно один мой сосед-рыцарь". Ефима за столом не было. Сколько рыцарей было за столом?
- У Ефима есть коллекция чисел, у которых первая цифра равна сумме второй и третьей, а третья цифра равна сумме второй и четвертой. Назовите самое маленькое число в коллекции Ефима.
- На столе в ряд стоят 9 тарелок с борщом. Ефим и Фома играют в игру "Съешь борщ". За один ход можно съесть суп либо из одной тарелки, либо из двух соседних. Проигрывает тот, кому нечего есть. Ефим очень хочет выиграть. Помогите ему!
- Четыре приятеля по дну высохшего озера собирали старинные монеты. На вопрос Ефима "Сколько монет вы вместе собрали?" они ответили так. Коля: "Не меньше ста". Вася: "Золотых - двадцать". Даша: "Вася ошибается". Паша: "Не больше 99". Сколько ребят сказали правду? Ответ объясните.
- У Ефима есть коллекция из 100 замечательных камней весом от 1 до 100 кг. На какое наименьшее число кучек их можно разделить так, чтобы ни в одной кучке не было двух
- камней, один из которых весит в 2 раза больше другого?
- У Ефима есть флажок. Крайне необходимо разрезать флажок на 4 части так, чтобы из этих частей можно составить развертку куба.

6 класс
читать дальше »
- Назовем фигуру, нарисованную на клетчатой бумаге по линиям сетки, "хорошей", если ее можно разрезать на доминошку в 2 клетки и уголок из 3 клеток. Ефим коллекционирует "нехорошие" фигуры. В "нехорошей" фигуре каждая клетка имеет хотя бы одну общую сторону с другой клеткой. Нарисуйте как можно больше "нехороших" фигур из 5 клеток для коллекции Ефима.
- 20% числа древних колес, собранных Ефимом, равны 80% числа древних колес, собранных Фомой. А всего у них 5 колес. Сколько древних колес у каждого?
- Ефима есть коллекция чисел, у которых первая цифра равна сумме второй и третьей, а третья цифра равна сумме второй и четвертой. Назовите самое маленькое число в коллекции Ефима.
- На столе стоят 10 тарелок с борщом. Ефим и Фома играют в игру "Съешь борщ". За один ход можно съесть суп либо из одной тарелки, либо из двух соседних. Проигрывает тот, кому нечего есть. Ефим очень хочет выиграть. Помогите ему!
- У Ефима есть флажок. Крайне необходимо разрезать флажок на 4 части так, чтобы из этих частей можно составить развертку куба. Как это сделать?

- Ефим пригласил на чаепитие 6 коллекционеров и посадил их за круглый стол. Каждый сидящий на четном месте гордо заявил: "Я - рыцарь!". Каждый сидящий на нечетном месте сказал: "Ровно один мой сосед-рыцарь". Ефима за столом не было. Сколько рыцарей было за столом?
- У Ефима есть коллекция из 100 замечательных камней весом от 1 до 100 кг. На какое наименьшее число кучек их можно разделить так, чтобы ни в одной кучке не было двух камней, один из которых весит в 2 раза больше другого?
- Дано 6 натуральных чисел. Все они различны и дают в сумме 22.Найти эти числа и доказать, что других нет.
7 класс
читать дальше »
- У Ефима есть коллекция чисел, у которых первая цифра равна сумме второй и третьей, а третья цифра равна сумме второй и четвертой. Назовите самое маленькое число в коллекции Ефима.
- На столе в ряд стоят 11 тарелок с борщом. Ефим и Фома играют в игру "Съешь борщ". За один ход можно съесть суп либо из одной тарелки, либо из двух соседних. Проигрывает тот, кому нечего есть. Ефим очень хочет выиграть. Помогите ему!
- В треугольнике АВС угол при вершине С равен 132 градусам, а при вершине В -12 градусам. Биссектрисы внешних углов В и С пересекают продолжения противоположных сторон в точках М и N соответственно. Докажите, что ВМ=СN.
- Дано 100 натуральных чисел. Все они различны и дают в сумме 5051. Найти эти числа и доказать, что других нет.
- Клетки квадрата 9х9 окрашены в красный и белый цвета. Докажите, что найдется или клетка, у которой ровно два красных соседа по углу, или клетка, у которой ровно два белых соседа по углу, или и то, и другое.
- На сторонах выпуклого четырехугольника АВСD отмечены точки P, Q, R, S так, что PQRS – прямоугольник, а P и R - середины сторон АВ и СD соответственно. Докажите, что площадь прямоугольника равна половине площади ABCD.
- Дано n попарно взаимно простых чисел, больших 1 и меньших (2n-1)x(2n-1). Докажите, что среди них обязательно есть простое число.
 |
 |
Примеры заданий |
23.09.2009 |
 |
Класс 1
читать дальше »
- Соедините 2 одинаковых рисунка
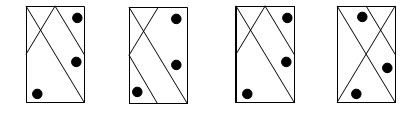
- Нарисуйте пропущенный рисунок

- Весы находятся в равновесии. Мяч весит 1 килограмм. Сколько весит кубик?
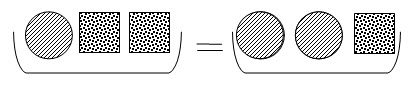
- Лена , Оля и Таня ели мороженое. Лена съела на 2 секунды раньше Оли, а Оля – на 1 секунду позже Тани. Кто съел мороженое раньше и насколько?
- Какие гирьки из имеющихся надо поставить на правую чашку весов, чтобы весы уравновесились? Нарисуйте их.
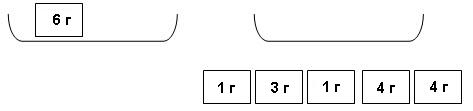
- У Маши, Светы и Тани вместе два мячика и кубик. У Маши и Светы разные предметы. Какой предмет у Тани?

Класс 2
читать дальше »
- Лена, Оля и Таня ели мороженое. Лена съела на 2 секунды раньше Оли, а Оля – на 1 секунду позже Тани. Кто съел мороженое раньше и насколько?
- Коля, Вася, Боря играли в шашки. Каждый сыграл по 2 партии. Сколько было сыгранно партий?
- Какие гирьки из имеющихся надо поставить на весы, что бы весы уравновесились? Ставить можно на обе чашки весов. Нарисуйте эти гирьки.
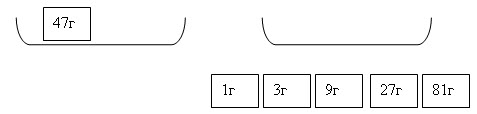
- Впишите в квадратики цифры, так что бы получилось верное равенство
- По краю круглого торта поставили 5 точек из крема на одинаковом расстоянии друг от друга. Через все пары точек сделали разрезы. Сколько получилось кусков?
- Три подряд идущие целые числа в сумме дают 93. Что это за числа?
Класс 4
читать дальше »
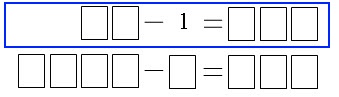
- Расставьте в кружочки числа от 1 до 7 так, чтобы сумму трёх чисел на каждой прямой была одинакова.
- Из Москвы в Саратов самолёт летит 2ч 30м. А из Саратова в Москву 150 минут. Как объяснить такую разницу?
- Сколько надо напечатать цифр, чтобы пронумеровать тетрадь, в которой 100 страниц?
- Три подряд идущие целые числа в сумме дают 93. Что это за числа?
- Чашка с водой весит 250 г. Когда воду перелили в бутылку, бутылка стала весить 210 г. Пустые чашка и бутылка вместе весят 160 г. Сколько весит вода?
- Из проволоки сложили квадрат со стороной 9 метро. Потом из этой же проволоки сложили треугольник, все стороны которого равны.. Какова длина одной стороны треугольника?
Разрезания
читать дальше »
Данное занятие является одним из первых. Оно направлено на развитие воображения, фантазии и пространственного мышления ребенка. На этом занятии не требуется применение каких-то специальных знаний, не надо делать сложные логические умозаключения, а ответом в задаче является просто пример разрезания.
Итак, рассматриваемой темой будут "разрезания", то есть, мы будем пытаться разбить клеточную фигуру на другие, более маленькие фигуры, возможно, с некоторыми ограничениями.
Далее приведены некоторые подсказки-рекомендации по решению задач данного типа.
- В каждой из предложенных ниже задач вы можете сразу посчитать количество клеток в маленькой фигуре, на которые, собственно, и требуется разрезать большую фигуру. Для этого достаточно всего лишь разделить общее количество клеточек в начальной фигуре на количество маленьких фигур. Подобную подсказку можно в какой-то момент дать и ребенку, если это требуется.
- После того, как вы нашли количество клеточек в начальной фигуре, вы можете легко перебрать все возможные виды этих фигур. Например, если вы посчитали, что фигура должна состоять из 3 клеток, то далее нетрудно убедиться, что существует всего два вида таких фигур, а именно "уголок", состоящий из 3 клеток, и "дощечка" размерами 1х3.
Задачки ребенку нужно давать по одной. Если задачу решить не получается, то нужно переходить к следующей задаче. Не должно ни в коем случае стоять цели решать все задачки подряд. Если Вы поможете решить задачу, то можно через какое-то время еще раз дать ее для полностью самостоятельного решения. Вы можете придумать еще несколько задач самостоятельно и попросить придумать несколько задач своего ребенка. Не забывайте, что занятия в таком возрасте – это, прежде всего, игра!
Когда ребенок решает задачи, постарайтесь не вмешивайтесь до того момента, пока малыш сам не попросит вас о помощи, если таковая потребуется.
Думаем, что не нужно давать больше 2-3 задач в день, часто достаточно решить одну, но самому.
Мы искренне надеемся, что наши задачи доставят Вам исключительно приятные впечатления и принесут огромную пользу Вам и Вашему ребенку.
Желаем успеха!
Пример решения задачи:
читать дальше »
Условие: Как разрезать фигуру на 3 одинаковые по форме части, чтобы в каждой из частей была красная клетка?
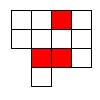
Решение:
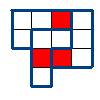
Посчитаем количество клеточек в маленькой фигуре. 12/3=4. Значит, нам необходимо разбивать на четырехклеточные фигуры. Далее строим пример разрезания.
Примеры задач:
читать дальше »
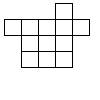
Задача №1:
Ослик ИА-ИА пытается разрезать фигуру на 3 одинаковые по форме части. Прибежал Пятачок и помог ослику. Как они это сделали?
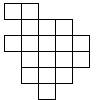
Задача №2:
Ослик Иа-Иа и Пятачок не могут разрезать фигуру на 3 одинаковые по форме части. Помогите им это сделать.
Задача №3:
Разрежьте фигуру на 3 неодинаковых прямоугольника (не забудьте показать, что такое прямоугольник и не забудьте, что квадрат – это тоже прямоугольник):

Задача №4:
Винни-Пух хочет разрезать фигуру на 4 одинаковые по форме части. Как ему это сделать?
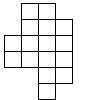
Задача №5:
Друг Винни-Пуха, Кролик, придумал, как можно разрезать фигуру на 4 различные фигуры, каждая из которых состоит из 4 клеток. А вы сможете?
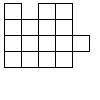
Над следующими двумя задачами думал весь волшебный лес. Сова сказала, что решить их невозможно, а Кристофер Робин сказал, что он знает, как их решить. Кто прав?
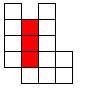
Задача №6:
Разрежьте фигуру на 3 одинаковых по форме части, таким образом, чтобы в каждой из 3-х частей была ровно одна красная клеточка:
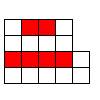
Задача №7:
Разрежьте фигуру на 6 одинаковых по форме частей, таким образом, чтобы в каждой из шести частей была ровно одна красная клеточка:
Задача №8:
"Научная проблема" (решение мы никому не скажем!).
Как в листе бумаги 10см на 20см ножницами прорезать дырку, чтобы в нее пролезла тумбочка 1м х 1м х 1м?
Дополнительные задачи. Если ребенку надоедят "разрезания", то эти задания можно дать решить между задачами 1-7.
- Винни-Пух пришел покупать книгу по математике. Продавец сказал, что книга стоит 100 рублей и еще половину стоимости книги. Сколько Винни-Пух заплатил за книгу?
- Как расставить скобки и знаки действий, чтобы из четырех пятерок получить 30?
- Как разрезать тремя прямолинейными разрезами круглый торт на 8 частей?
Желаем успехов!!!
Решения
читать дальше »
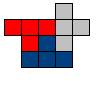
Задача №1:
Ослик Иа-Иа пытается разрезать фигуру на 3 одинаковые по форме части. Прибежал Пятачок и помог ослику. Как они это сделали?
Решение:
Задача №2:
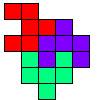
Ослик Иа-Иа и Пятачок не могут разрезать фигуру на 3 одинаковые по форме части. Помогите им это сделать.
Решение:
Задача №3:
Разрежьте фигуру на 3 неодинаковых прямоугольника (не забудьте показать, что такое прямоугольник и не забудьте, что квадрат – это тоже прямоугольник):
Решение:

Задача №4:
Винни-Пух хочет разрезать фигуру на 4 одинаковые по форме части. Как ему это сделать?
Решение:

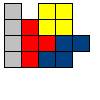
Задача №5:
Друг Винни-Пуха, Кролик, придумал, как можно разрезать фигуру на 4 различные фигуры, каждая из которых состоит из 4 клеток. А вы сможете?
Решение:
В следующих задачах некоторые клеточки были помечены красным цветом, в решении они помечены крестиком.
Задача №6:
Разрежьте фигуру на 3 одинаковые по форме части, таким образом, чтобы в каждой из 3-х частей была ровно одна красная клеточка(клеточка с крестиком):
Решение:
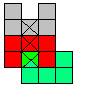
Задача №7:
Разрежьте фигуру на 6 одинаковых по форме частей, таким образом, чтобы в каждой из шести частей была ровно одна красная клеточка (клеточка с крестиком):
Решение:

Дополнительные задачи
читать дальше »
- Винни-Пух пришел покупать книгу по математике. Продавец сказал, что книга стоит 100 рублей и еще половину стоимости книги. Сколько Винни-Пух заплатил за книгу?
Решение:
Книга стоит 200 рублей, так 100 рублей – это ровно половина стоимости книги.
- Как расставить скобки и знаки действий, чтобы из четырех пятерок получить 30?
Решение:
(5:5+5)·5=30.
- Как разрезать тремя прямолинейными разрезами круглый торт на 8 частей?
Решение:
Нужно сделать два разреза крест-накрест, получится 4 части. И еще один разрез параллельно столу, получится 8 частей.
|
|