Математика: Свойства функций

Свойства функций

Свойства функции разберем на примере о графика произвольной функции y = f (x):

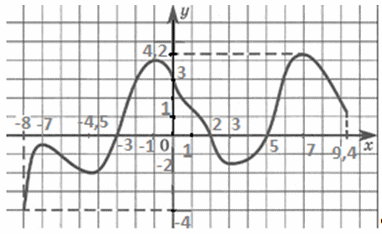
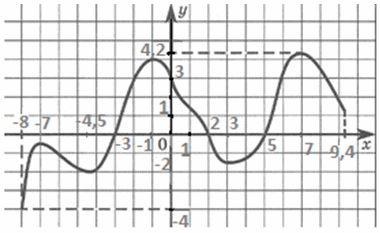
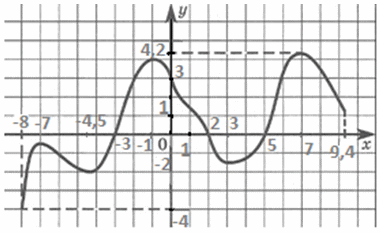
Область определения функции — это множество всех значений переменной x, которые имеют соответствующие им значения функции. Обозначают: D(f).На графике область определения — это промежутки на оси ОX, над которыми (или под которыми) имеются части графика. Для нашего примера D(f) = [-8; 9,4].
Область значений функции — это множество всех ее значений у. Обозначают: E(f).На графике область значений функции — это промежутки на оси OY, слева или справа от которых (в горизонтальной полосе) находятся части графика.Для нашего примера Е(f) = [-4; 4,2].
Функция y = f (x) называется возрастающей, если для любой пары значений аргументов x₁, x₂ из неравенства x₁ < x₂ следует неравенство f (x₁) < f (x₂).Функцию можно назвать возрастающей на промежутке, если большему из любых двух взятых из него чисел всегда соответствует большее значение функции.Для нашего примера функция возрастает при 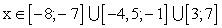.Функция y = f (x) называется убывающей, если для любой пары значений аргументов x₁, x₂ из неравенства x₁ < x₂ следует неравенство f (x₁) > f (x₂).Функцию можно назвать убывающей на промежутке, если из любых двух взятых из него чисел большему из них всегда соответствует меньшее значение функции.Для нашего примера функция убывает при .
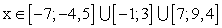Промежутки знакопостоянства — промежутки, на которых значения функции имеют постоянный знак (положительный или отрицательный).Промежуток положительного знака — это множество значений переменной x, у которых соответствующие значения функции больше нуля (y > 0).На графике — это части оси абсцисс, у которых соответствующие кусочки графика выше оси ОХ. Без графика их тоже можно найти, составив и решив неравенство f (x) > 0.Для нашего примера функция положительна при 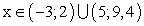.Промежуток отрицательного знака — это множество тех значений переменной х, у которых соответствующие значения функции меньше нуля (y < 0).На графике — это промежутки оси абсцисс, у которых соответствующие кусочки графика ниже оси ОХ. Без графика их тоже можно найти, составив и решив неравенство f (x) < 0.Для нашего примера функция отрицательна при .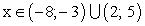
Нули функции — это значения переменной х, при которых у (х) = 0.Без графика нули функции тоже можно найти, составив и решив уравнение f (x) = 0.По графику нули определяют как абсциссы точек пересечения графика с осью ОХ.Для нашего примера нули функции это точки х₁ = -3, х₂ = 2, х₃ = 5.
Четность и нечетность функции.Функция называется четной, если ее график симметричен относительно оси ОУ и для любого x ϵ D(f) верно: -х ϵ D(f) и f (-x) = f (x).Т.е. функция называется четной, если любым двум противоположным значениям аргумента, из области определения, соответствуют равные значения функции.На графике четная функция имеет ось симметрии OY.Функция называется нечетной, если ее область определения симметрична относительно нуля и для любого x ϵ D(f) верно: -х ϵ D(f) и f (-x) = -f (x).Т.е. функция называется нечетной, если любым двум противоположным значениям аргумента соответствуют противоположные значения функции.На графике нечетная функция симметрична относительно начала координат.Произведение или частное двух четных функций — есть функция четная.Произведение или частное двух нечетных функций — есть функция четная.Произведение или частное двух функций, одна из которых четная, а другая нечетная — есть функция нечетная.Функция нашего примера — ни четная, ни нечетная.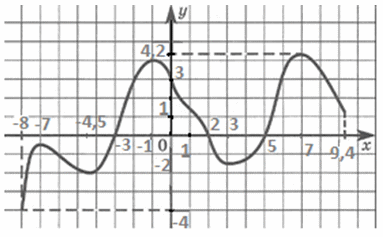
Периодичность функции.Функция y = f (x) называется периодической с периодом Т > 0, если для любого x ϵ D(f) верно: (х — Т) ϵ D(f), (х + Т) ϵ D(f) и f (х — Т) = f (х + Т) = f (x).Если Т > 0 является периодом функции y = f (x), то число 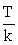— период функции y = f (kx + b).Если Т₁ > 0 и Т₂ > 0 — периоды соответствующих функций y = f (x) и y = g (x), причем 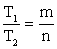, где m, n ϵ N, , то любая комбинация этих функций y = a • f (x) + b • g(x), a, b ϵ Z, также периодическая, период которой равен T = HOK(T₁, T₂).Функция нашего примера не является периодической.
Точки экстремума функции (точки максимума и минимума).Точка х₀ называется точкой минимума, если для всех х ϵ D(f) в некоторой окрестности этой точки выполняется равенство f (x) ≥ f (x₀).На графике точки минимума — это абсциссы, в которых график выглядит как «ямка».Для нашего примера точки минимума — это х₁ = -4,5, х₂ = 3.Точка х₀ называется точкой максимума, если для всех х ϵ D(f) в некоторой окрестности этой точки выполняется равенство f (x) ≤ f (x₀).На графике точки максимума — это абсциссы, в которых график выглядит как «горка».Для нашего примера точки максимума — это х₁ = -7, х₂ = -1, х₃ = 7.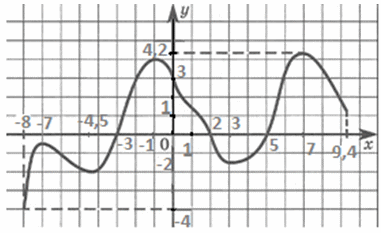
Наименьшее и наибольшее значение функции.Число y = t называется наименьшим значением функции на промежутке [a, b], если для любого значения аргумента х ϵ [a, b] из этого промежутка верно неравенство t ≥ f (x).Для нашего примера наибольшее значение функции на промежутке [-8; 9,4] равно у_н/б = 4,2.Число y = t называется наибольшим значением функции на промежутке [a, b], если для любого значения аргумента х ϵ [a, b] из этого промежутка верно неравенство t ≤ f (x).Для нашего примера наименьшее значение функции на промежутке [-8; 9,4] равно у_н/м = -4.

Свойства элементарных функций

Линейная функция f (x) = kx + b.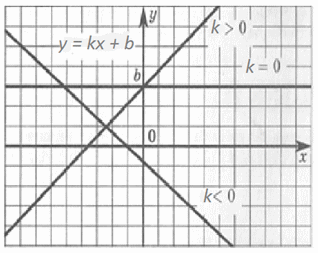D(f) = R, E(f) = R.График функции y = kx + b — прямая линия. Функция монотонно возрастает при k > 0 и убывает при k < 0. При b = 0 прямая линия проходит через начало координат, при этом функция y = kx — нечетная. Промежутки постоянного знака для функции y = kx зависят от знака параметра k:k > 0, то y > 0 при x > 0; y < 0 при x < 0;k < 0, то y > 0 при x < 0; y < 0 при x > 0.

Квадратичная функция

f(x) = ах² + bх + с, а ≠ 0. Графиком является парабола.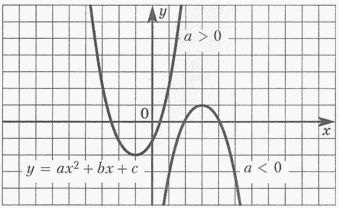

Функция
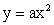
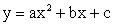
Область определения	R	R
Вершина параболы	(0; 0)
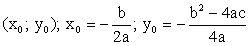
Нули функции	x = 0
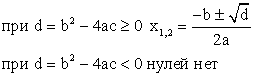
Экстремумы	если a < 0, то минимум в вершине если a > 0, то максимум в вершине
Область значений
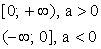
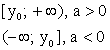
Четность	четная	ни четная, ни нечетная

Степенная функция

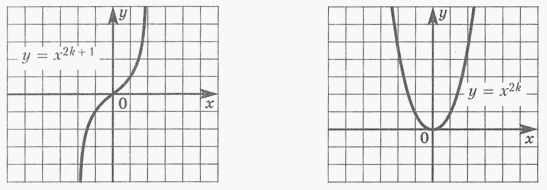
f (x) = хⁿ, n ≥ 2, n ϵ N. Графиками ее являются квадратичные

или кубические параболы

Функция
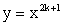
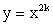
Область определения	R	R
Область значений	R	[0; +∞ )
Четность	нечетная	четная
Нули функции	х =0	х =0
Экстремумы	нет	х = 0 — точка минимума
Монотонность	возрастает при х ϵ R	при х ≤ 0 убывает при х > 0 возрастает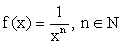

— частный случай дробно-рациональной функции

. Графиками ее являются гиперболы соответствующей степени. Заметим, что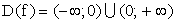

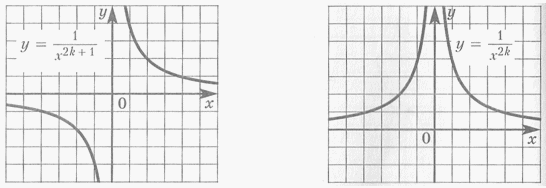
Функция
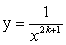
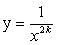
Область определения	R кроме х = 0	R кроме х = 0
Область значений	(-∞ ; 0) U (0; +∞ )	(0; +∞ )
Четность	нечетная	четная
Нули функции	нет	нет
Экстремумы	нет	нет
Монотонность	убывает при x ϵ D(f)	при х < 0 возрастает при х > 0 убывает

Степенная функция

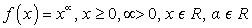
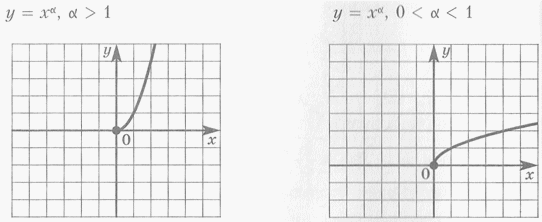
Функция
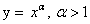
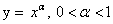
Область определения
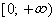
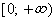
Область значений
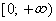
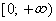
Нули функции	х = 0	х = 0
Экстремумы	нет	нет
Монотонность	возрастает при х ϵ D(f)	возрастает при х ϵ D(f)

Показательная функция

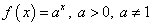
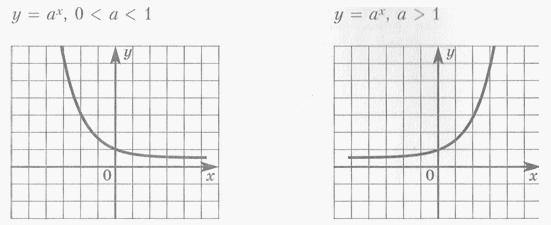
Функция	y = a^x, 0 < a < 1	y = a^x, a > 1
Область определения	R	R
Область значений	( 0; +∞ )	( 0; +∞ )
Нули функции	нет	нет
Экстремумы	нет	нет
Монотонность	убывает при х ϵ D ( f )	возрастает при х ϵ D ( f )

Логарифмическая функция

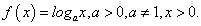
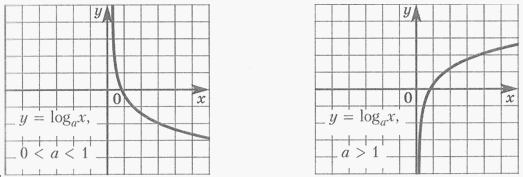
Функция	y = log_ax, 0 < a < 1	y = log_ax, a > 1
Область определения	( 0; +∞)	( 0; +∞)
Область значений	R	R
Нули функции	нет	нет
Экстремумы	нет	нет
Монотонность	убывает при х ϵ D ( f )	возрастает при х ϵ D ( f )

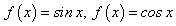— тригонометрические функции

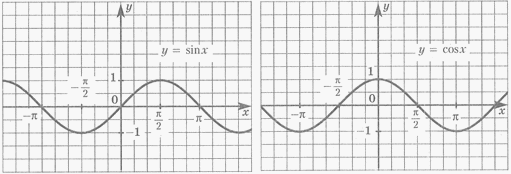
Функция	y = sin x	y = cos x
Область определения	R	R
Область значений	[-1; 1 ]	[-1; 1 ]
Нули функции
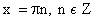
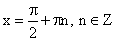
Четность	нечетная	четная
Периодичность
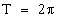
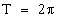
Экстремумы
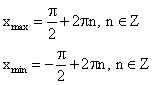
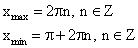
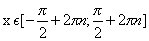
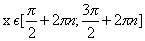
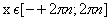
Монотонность	возрастает при убывает при	возрастает при убывает при

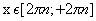
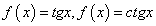— тригонометрические функции.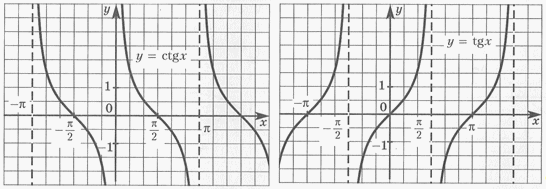

Функция	y = tg x	y = ctg x
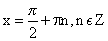
Область определения	R кроме	R кроме
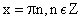
Область значений	R	R
Нули функции
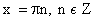
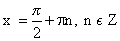
Четность	нечетная	нечетная
Периодичность
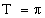
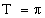
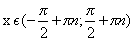
Монотонность	возрастает при	убывает при

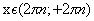
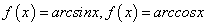— обратные тригонометрические функции

Функция	y = arcsin x	y = arcos x
Область определения	[-1; 1 ]	[-1; 1 ]
Область значений
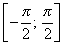
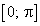
Нули функции	x = 0	x = 1
Четность	нечетная	ни четная, ни нечетная
Монотонность	возрастает при x ϵ [-1; 1 ]	убывает при x ϵ [ -1 ; 1 ]

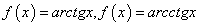— обратные тригонометрические функции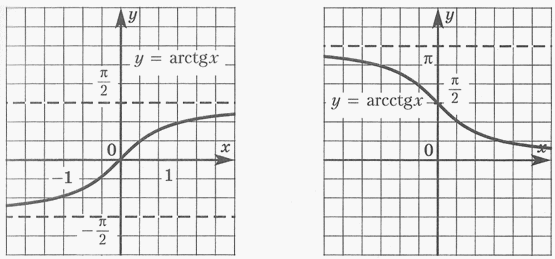

Функция	y = arctg x	y = arcctg x
Область определения	R	R
Область значений
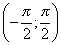
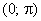
Нули функции	x = 0	нет
Четность	нечетная	нечетная
Монотонность	возрастает при x ϵ R	убывает при x ϵ R

Иррациональные функции

вида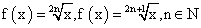

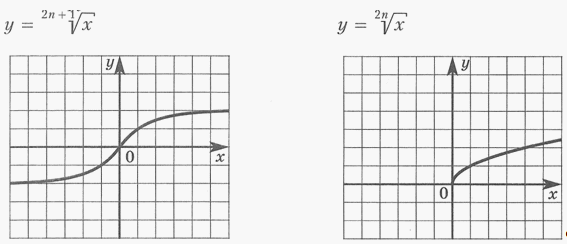
Функция
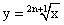
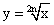
Область определения	R	[0; +∞ )
Область значений	R	[0; +∞ )
Нули функции	х = 0	х = 0
Экстремумы	нет	нет
Монотонность	возрастает при х ϵ D ( f )	возрастает при х ϵ D ( f )

Обратные функцииОбратимой

называют функцию, принимающую каждое свое значение в единственной точке области определения.Например, у = х² необратима на R, т.к. уравнение f (х) = х² имеет два решения: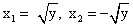

. Однако, у = х² обратима на множестве х ≥ 0 или на множестве х ≤ 0, где выполняется единственность решения.Функцию f^-1(x) называют обратной к функции f (x), если функция f^-1(x) в каждой точке области значений обратимой функции f принимает такое значение у, что f (y) = x.Например, функцией, обратной к функции f (x) = kx + b, является функция:

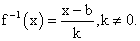Свойства обратных функций

Область значений функции f^-1(x) является областью определения функции f (x).E(f^-1(x)) = D(f), E(f) = D(f^-1(x)).
Графики функции f (x) и обратной к ней f^-1(x) симметричны относительно биссектрисы у = х.
Если функция f (x) монотонна на промежутке Х, то она обратима на этом промежутке.
Если функция f (x) возрастает (убывает) в своей области определения, то и обратная к ней f^-1(x) тоже возрастает (убывает).

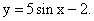Пример 1.Найти область значений функции

РешениеПо определению синуса: -1 ≤ sinx ≤ 1. Умножим данное неравенство на 5:-5 ≤ 5sin x ≤ 5, затем вычтем из всех частей неравенства 2, получим: -7 ≤ 5sin x — 2 ≤ 3.Ответ: [-7; 3].Пример 2.Указать множество значений функции y = 5 — 2^х

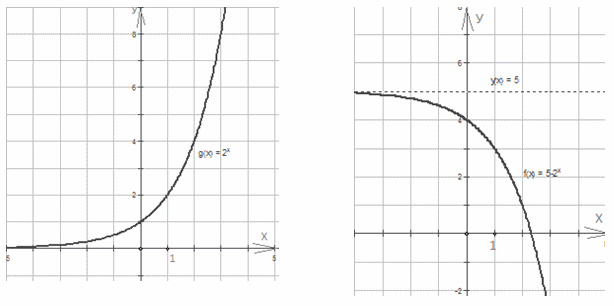Решение1-й способ.Симметрично оси ОХ отобразим график показательной функции у = 2^х, чтобы получить график у = -2^х. Затем последнюю функцию поднимем на 5 единиц вверх по оси ОУ. Видим, что область значений нашей функции — это луч (-∞; 5).2-й способ.2^х > 0. Умножим данное неравенство на (-1), получим -2^х < 0. Прибавим к обеим частям неравенства 5, получим 5 — 2^х < 5. Т.е. Е (у) = (-∞; 5).Ответ: (-∞; 5).Пример 3.Найти область определения функции

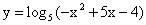РешениеПо определению логарифмической функции -х² + 5х — 4 > 0. По теореме, обратной к теореме Виета, найдем корни квадратного уравнения: х₁ = 1, х₂ = 4 и разложим квадратный трехчлен на множители: -(х — 1)(х — 4) > 0. Применяя метод интервалов для решения неравенства, получим х ϵ (1; 4).Ответ: (1; 4).Пример 4.Найти множество значений функции

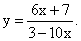РешениеВыразим х через у: 6х + 7 = 3у — 10ху; х(6 + 10у) = 3у — 7.Если 6 + 10у = 0, то у = -0,6. Подставляя это значение у в последнее уравнение, получим:0х = -8,8. Данное уравнение корней не имеет, значит, функция

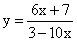не принимает значения равного -0,6.Если 6 + 10у ≠ 0, то

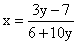. Область определения последнего уравнения — любое действительное у, кроме у = -0,6. Получаем, что Е(у) = (-∞; -0,6) U (-0,6; +∞).Ответ: (-∞; -0,6) U (-0,6; +∞).Пример 5.Найти множество значений функции

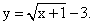РешениеУчитывая, что

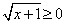, по свойствам неравенств получим

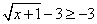. Т.е. Е (у) = [-3; +∞).Ответ: [-3; +∞).Пример 6.Найти множество значений функции

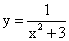РешениеТак как Е(х²) = [0; +∞), то Е(х² + 3) = [3; +∞). Так как обратная пропорциональность — непрерывная и убывающая функция на этом промежутке, большему значению аргумента будет соответствовать меньшее значение функции. При стремлении аргумента этой функции к +∞ значение самой функции стремится к нулю: Е (1 / (х² + 3)) = (0; 1/3].Ответ: (0; 1/3].Пример 7.Найти множество значений функции

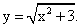РешениеЕ(х²) = [0; +∞), Е(х² + 3) = [3; +∞). Так как функция

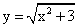непрерывна и возрастает на этом промежутке, то

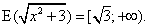Ответ:

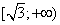.Пример 8.Найти наименьшее значение функции

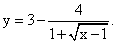РешениеРазность принимает наименьшее значение при наибольшем значении вычитаемого. Дробь принимает наибольшее значение при наименьшем значении знаменателя. Получаем, что данная функция принимает наименьшее значение при наименьшем значении выражения

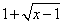, находящегося в знаменателе дроби.

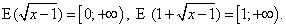Итак, наименьшее значение знаменателя равно 1. Тогда функция принимает значение, равное -1.Ответ: -1.Список используемой литературы Видеолекция «Свойства функций»:

Перейти к выполнению теста: Тест. Свойства функций