Треугольник
 ».В произвольном треугольнике.
».В произвольном треугольнике.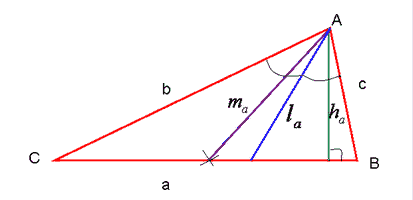 Медианой треугольника
Медианой треугольника (
(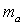 )называют отрезок, соединяющий вершину треугольника с серединой противоположной стороны.Длина медианы треугольника выражается формулой:
)называют отрезок, соединяющий вершину треугольника с серединой противоположной стороны.Длина медианы треугольника выражается формулой: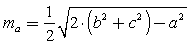 .Длина стороны треугольника через медианы выражается формулой:
.Длина стороны треугольника через медианы выражается формулой: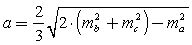 .Биссектрисой треугольника
.Биссектрисой треугольника (
(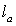 )называют отрезок прямой, заключенной между вершиной и точкой ее пересечения с противоположной стороной, которая делит угол пополам.Длина биссектрисы треугольника выражается формулой:
)называют отрезок прямой, заключенной между вершиной и точкой ее пересечения с противоположной стороной, которая делит угол пополам.Длина биссектрисы треугольника выражается формулой: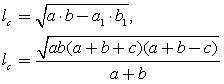 .Высота треугольника
.Высота треугольника  (
(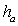 ) – это отрезок перпендикуляра, опущенного из вершины треугольника на противоположную сторону, или на ее продолжение.Длина высоты:
) – это отрезок перпендикуляра, опущенного из вершины треугольника на противоположную сторону, или на ее продолжение.Длина высоты: 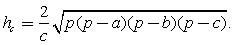 Признаки равенства треугольников:
Признаки равенства треугольников:- по двум сторонам и углу между ними;
- по стороне и двум прилегающим к ней углам;
- по трем сторонам.
 треугольника ABC при вершине A называется угол, смежный углу треугольника при вершине A.Сумма внутренних углов
треугольника ABC при вершине A называется угол, смежный углу треугольника при вершине A.Сумма внутренних углов треугольника:
треугольника:- сумма любых двух углов треугольника меньше
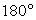 ;
; - в каждом треугольнике два угла острые;
- внешний угол треугольника больше любого внутреннего угла, не смежного с ним;
- сумма углов треугольника равна
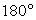 ;
; - внешний угол треугольника равен сумме двух других углов, не смежных с ним;
- сумма острых углов прямоугольного треугольника равна
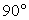 .
.
 .Средняя линия треугольника обладает свойством – она параллельна основанию треугольника и равна ее половине.Средняя линия треугольника отсекает от треугольника ему подобный треугольник.Площадь отсекаемого треугольника относится к площади основного треугольника в отношении 1:4.Свойства серединного перпендикуляра
.Средняя линия треугольника обладает свойством – она параллельна основанию треугольника и равна ее половине.Средняя линия треугольника отсекает от треугольника ему подобный треугольник.Площадь отсекаемого треугольника относится к площади основного треугольника в отношении 1:4.Свойства серединного перпендикуляра отрезка:
отрезка: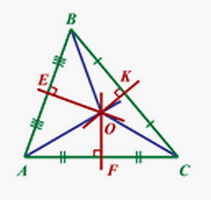
- точка лежащая на серединном перпендикуляре одинаково удалена от концов отрезка;
- любая точка, одинаково удаленная от концов отрезка, лежит на серединном перпендикуляре.
- любая точка, лежащая на биссектрисе угла, одинаково удалена от сторон угла;
- любая точка, одинаково удаленная от сторон угла, лежит на биссектрисе угла.
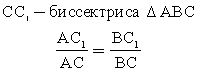 Три медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины треугольника.
Три медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины треугольника.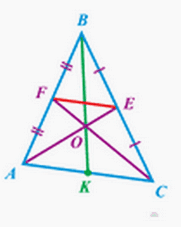 Теорема косинусов
Теорема косинусов . В любом треугольнике, квадрат стороны равен сумме квадратов двух других сторон без их удвоенного произведения на косинус угла между ними:
. В любом треугольнике, квадрат стороны равен сумме квадратов двух других сторон без их удвоенного произведения на косинус угла между ними: 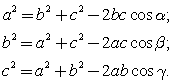 Теорема синусов
Теорема синусов . Стороны треугольника пропорциональны синусам противоположных углов:
. Стороны треугольника пропорциональны синусам противоположных углов: 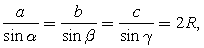 где R — радиус окружности, описанной около этого треугольника.Пусть a, b, c — стороны;
где R — радиус окружности, описанной около этого треугольника.Пусть a, b, c — стороны; 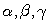 — противолежащие им углы; p — полупериметр; R — радиус описанной окружности; r — радиус вписанной окружности; S — площадь;
— противолежащие им углы; p — полупериметр; R — радиус описанной окружности; r — радиус вписанной окружности; S — площадь; 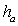 — высота, проведенная к стороне a.
— высота, проведенная к стороне a.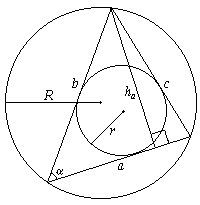 Площадь треугольника
Площадь треугольника равна половине произведения стороны на высоту, опущенную на эту сторону (или половине произведения сторон на синус угла между ними).Треугольник называется прямоугольным
равна половине произведения стороны на высоту, опущенную на эту сторону (или половине произведения сторон на синус угла между ними).Треугольник называется прямоугольным , если у него есть прямой угол. В прямоугольном треугольнике сторона, противоположная прямому углу, называется гипотенузой
, если у него есть прямой угол. В прямоугольном треугольнике сторона, противоположная прямому углу, называется гипотенузой . Остальные две стороны, называются катетами
. Остальные две стороны, называются катетами .Катет прямоугольного треугольника есть средняя пропорциональная величина между гипотенузой и проекцией этого катета на гипотенузу:
.Катет прямоугольного треугольника есть средняя пропорциональная величина между гипотенузой и проекцией этого катета на гипотенузу: 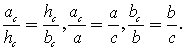 Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между проекциями катетов на гипотенузу:
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между проекциями катетов на гипотенузу: 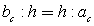 или
или 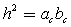 .Теорема Пифагора
.Теорема Пифагора . В прямоугольном треугольнике, квадрат гипотенузы равен сумме квадратов катетов:
. В прямоугольном треугольнике, квадрат гипотенузы равен сумме квадратов катетов: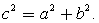 В прямоугольном треугольнике, медиана, проведенная к гипотенузе, делит треугольник на два равновеликих треугольника.Соотношения между сторонами и углами в прямоугольном треугольнике
В прямоугольном треугольнике, медиана, проведенная к гипотенузе, делит треугольник на два равновеликих треугольника.Соотношения между сторонами и углами в прямоугольном треугольнике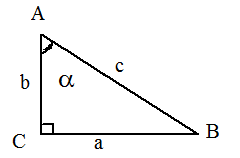
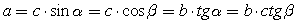 .Прямоугольный треугольник.a, b — катеты; c — гипотенуза;
.Прямоугольный треугольник.a, b — катеты; c — гипотенуза; 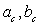 — проекции катетов на гипотенузу:
— проекции катетов на гипотенузу: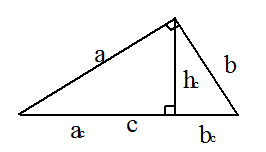
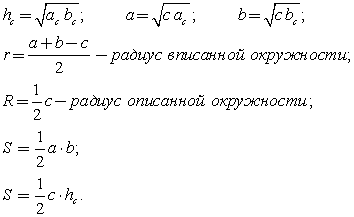 Свойства сторон и углов прямоугольного треугольника:
Свойства сторон и углов прямоугольного треугольника:- углы, противолежащие катетам — острые;
- гипотенуза больше любого из катетов;
- сумма катетов больше гипотенузы.
- по катету и острому углу;
- по двум катетам;
- по гипотенузе и катету;
- по гипотенузе и острому углу.
 , если у него две стороны равны.Свойства равнобедренного треугольника:
, если у него две стороны равны.Свойства равнобедренного треугольника:- в равнобедренном треугольнике углы при основании равны;
- если в треугольнике два угла равны, то он равнобедренный;
- в равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой;
- если в треугольнике медиана и биссектриса (или высота и биссектриса, или медиана и высота), проведенная из какой-либо вершины, совпадают, то такой треугольник равнобедренный.
 . В равностороннем треугольнике все углы равны
. В равностороннем треугольнике все углы равны 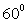 . Каждая из трех высот является также биссектрисой и медианой.Равносторонний треугольник:
. Каждая из трех высот является также биссектрисой и медианой.Равносторонний треугольник: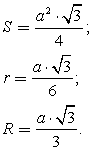 Существование окружности, описанной около треугольника:
Существование окружности, описанной около треугольника:- все три серединные перпендикуляры треугольника пересекаются в одной точке и эта точка является центром описанной окружности. Описанная около треугольника окружность всегда существует и она единственна;
- центром описанной окружности прямоугольного треугольника является середина гипотенузы.
- все три биссектрисы треугольника пересекаются в одной точке и эта точка является центром вписанной окружности;
- вписанная в треугольник окружность всегда существует и она единственна.
- по двум углам;
- по двум пропорциональным сторонам и углу между ними;
- по трем пропорциональным сторонам.
- по острому углу;
- по пропорциональным катетам;
- по пропорциональным катету и гипотенузе.
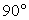 , AB=10, BC=8. Найдите cosA.Решение.
, AB=10, BC=8. Найдите cosA.Решение.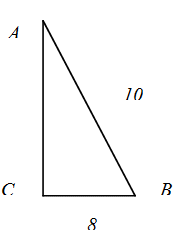 Для нахождения cosA необходимо воспользоваться определением косинуса острого угла прямоугольного треугольника. В рассматриваемом треугольнике
Для нахождения cosA необходимо воспользоваться определением косинуса острого угла прямоугольного треугольника. В рассматриваемом треугольнике 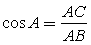 , где АС — прилежащий катет, АВ — гипотенуза.Вычислим катет АС. Для этого применим теорему Пифагора:
, где АС — прилежащий катет, АВ — гипотенуза.Вычислим катет АС. Для этого применим теорему Пифагора: 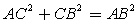 , тогда
, тогда 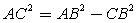 , тогда
, тогда 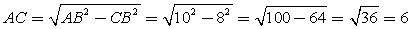 .Окончательно получаем
.Окончательно получаем 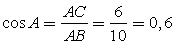 .Ответ: 0,6.Пример 2.На клетчатой бумаге с клетками размером
.Ответ: 0,6.Пример 2.На клетчатой бумаге с клетками размером 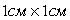 изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.
изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.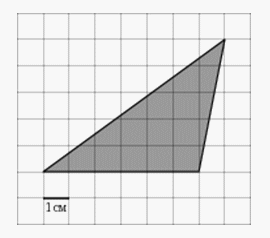 Решение.Воспользуемся формулой площади треугольника через сторону и высоту, проведенную к стороне:
Решение.Воспользуемся формулой площади треугольника через сторону и высоту, проведенную к стороне: 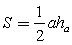 , где а — сторона,
, где а — сторона, 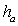 — высота, проведенная к стороне а. Данная задача имеет следующую особенность: высота, проведенная из правой вершины треугольника располагается вне самого треугольника. Однако и в данном случае будет справедлива формула
— высота, проведенная к стороне а. Данная задача имеет следующую особенность: высота, проведенная из правой вершины треугольника располагается вне самого треугольника. Однако и в данном случае будет справедлива формула 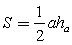 .Обратимся к рисунку: высота треугольника равна 5 см (располагается в данном случае вертикально и равна пяти клеткам), сторона (основание, располагается горизонтально) равна 6 см.Вычислим далее площадь треугольника:
.Обратимся к рисунку: высота треугольника равна 5 см (располагается в данном случае вертикально и равна пяти клеткам), сторона (основание, располагается горизонтально) равна 6 см.Вычислим далее площадь треугольника: 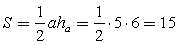 см.Ответ: 15.Пример 3.На клетчатой бумаге с клетками размером
см.Ответ: 15.Пример 3.На клетчатой бумаге с клетками размером 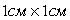 изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.
изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.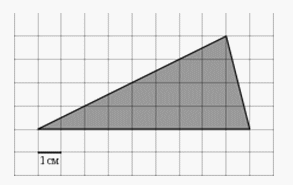 Решение.Воспользуемся формулой площади треугольника через сторону и высоту, проведенную к стороне:
Решение.Воспользуемся формулой площади треугольника через сторону и высоту, проведенную к стороне: 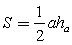 , где а — сторона,
, где а — сторона, 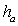 — высота, проведенная к стороне а.Анализируя рисунок, заметим, что высота треугольника равна 4 см (располагается в данном случае вертикально и равна четырем клеткам), сторона (основание, располагается горизонтально) равна 9 см.Переходим к вычислению площади:
— высота, проведенная к стороне а.Анализируя рисунок, заметим, что высота треугольника равна 4 см (располагается в данном случае вертикально и равна четырем клеткам), сторона (основание, располагается горизонтально) равна 9 см.Переходим к вычислению площади: 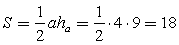 см.Ответ: 18.Пример 4.Площадь треугольника ABC равна 30 см2. На стороне AC взята точка D так, что AD:DC=2:3. Длина перпендикуляра DE, проведенного на сторону BC, равна 9 см. Найти BC.Решение.Проведем BD (см. рис.);
см.Ответ: 18.Пример 4.Площадь треугольника ABC равна 30 см2. На стороне AC взята точка D так, что AD:DC=2:3. Длина перпендикуляра DE, проведенного на сторону BC, равна 9 см. Найти BC.Решение.Проведем BD (см. рис.);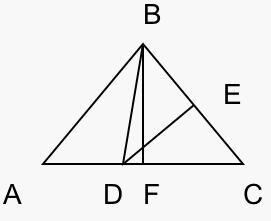 треугольники ABD и BDC имеют общую высоту BF; следовательно, их площади относятся как длины оснований, т.е.:
треугольники ABD и BDC имеют общую высоту BF; следовательно, их площади относятся как длины оснований, т.е.: 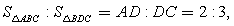 откуда
откуда 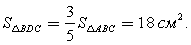 С другой стороны
С другой стороны 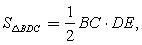 или
или 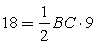 , откуда BC=4 см.Ответ: BC=4 см.Пример 5. В равнобедренном треугольнике высоты, проведенные к основанию и к боковой стороне, равны 10 и 12 см, соответственно. Найти длину основания.Решение.В ABC имеем AB=BC,
, откуда BC=4 см.Ответ: BC=4 см.Пример 5. В равнобедренном треугольнике высоты, проведенные к основанию и к боковой стороне, равны 10 и 12 см, соответственно. Найти длину основания.Решение.В ABC имеем AB=BC, 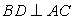 ,
, 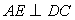 , BD=10 см и AE=12 см (см. рис.).
, BD=10 см и AE=12 см (см. рис.).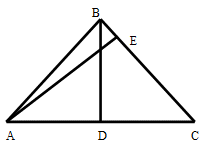 Пусть
Пусть 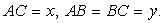 Прямоугольные треугольники AEC и BDC подобны (угол C общий); следовательно,
Прямоугольные треугольники AEC и BDC подобны (угол C общий); следовательно, 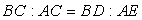 или
или 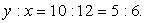 Применяя теорему Пифагора к BDC, имеем
Применяя теорему Пифагора к BDC, имеем 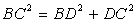 , т.е.
, т.е. 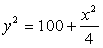 .В итоге, мы получили систему уравнений:
.В итоге, мы получили систему уравнений: 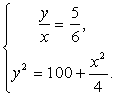 Решая эту систему, получим
Решая эту систему, получим 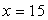 . Итак AC=15 см.Ответ: AC=15 см.Пример 6. В треугольнике ABC, AВ=5 см,
. Итак AC=15 см.Ответ: AC=15 см.Пример 6. В треугольнике ABC, AВ=5 см, 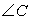 равен
равен 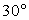 . Найти радиус описанного круга.Решение.
. Найти радиус описанного круга.Решение.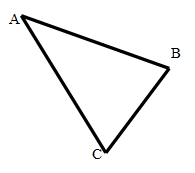 По теореме синусов имеем
По теореме синусов имеем 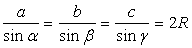 .Значит
.Значит 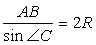 , т.е.
, т.е. 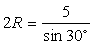 .Последовательно находим
.Последовательно находим 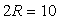 , т.е.
, т.е. 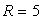 см.Ответ:
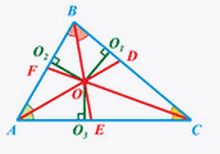
см.Ответ: 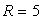 см.Пример 7. Внутри правильного треугольника со стороной a расположены три равные окружности, каждая из которых касается двух сторон треугольника и двух других окружностей. Найти площадь части треугольника, расположенной вне этих окружностей.
см.Пример 7. Внутри правильного треугольника со стороной a расположены три равные окружности, каждая из которых касается двух сторон треугольника и двух других окружностей. Найти площадь части треугольника, расположенной вне этих окружностей.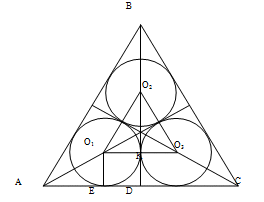 Решение.Пусть AB = BC = AC = a.Обозначим O1E = O1K = ED = r, тогда AD = AE + ED = AE + r =
Решение.Пусть AB = BC = AC = a.Обозначим O1E = O1K = ED = r, тогда AD = AE + ED = AE + r =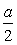 .AO1 — биссектриса угла A, следовательно,
.AO1 — биссектриса угла A, следовательно, 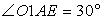 и в прямоугольном
и в прямоугольном 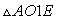 имеем AO1 = 2O1E = 2r и
имеем AO1 = 2O1E = 2r и 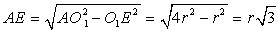 . Тогда AE + r =
. Тогда AE + r =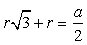 , откуда
, откуда 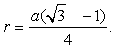
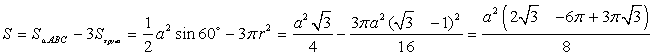 Ответ:
Ответ: 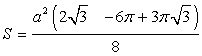 .Пример 8.Стороны треугольника равны 12 м, 16 м и 20 м. Найдите его высоту, проведенную из вершины большего угла.Решение.
.Пример 8.Стороны треугольника равны 12 м, 16 м и 20 м. Найдите его высоту, проведенную из вершины большего угла.Решение.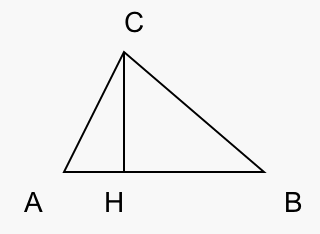 202 = 122 + 162400 = 144 + 256400 = 400 верно, следовательно,
202 = 122 + 162400 = 144 + 256400 = 400 верно, следовательно, 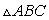 – прямоугольный (по теореме, обратной теореме Пифагора)
– прямоугольный (по теореме, обратной теореме Пифагора)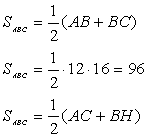 96 = 10 ВНВН = 9,6Ответ: ВН = 9,6.Пример 9.В прямоугольный треугольник вписан квадрат, имеющий с ним общий угол. Найдите площадь квадрата, если катеты треугольника равны 10 м и 15 м.Дано:
96 = 10 ВНВН = 9,6Ответ: ВН = 9,6.Пример 9.В прямоугольный треугольник вписан квадрат, имеющий с ним общий угол. Найдите площадь квадрата, если катеты треугольника равны 10 м и 15 м.Дано: 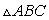 – прямоугольный, AC = 15, CB = 10Найти: SCDEF.
– прямоугольный, AC = 15, CB = 10Найти: SCDEF. Решение.
Решение.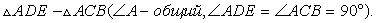 Пусть DE = DC = X, тогда AD = 15 – X
Пусть DE = DC = X, тогда AD = 15 – X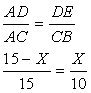 15 X = 10(15 – X)15 X = 150 – 10 X25 X = 150X = 6DE = DC = 6S кв. = 6 6 = 36Ответ: S кв. = 36 Видеолекция «Треугольник»:
15 X = 10(15 – X)15 X = 150 – 10 X25 X = 150X = 6DE = DC = 6S кв. = 6 6 = 36Ответ: S кв. = 36 Видеолекция «Треугольник»: 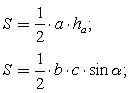
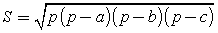 — формула
— формула 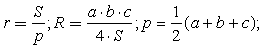
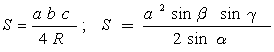 ,
,
